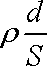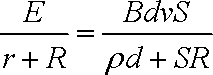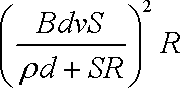- 带电粒子在匀强磁场中的运动
- 共240题
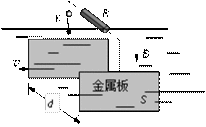
法拉第曾提出一种利用河流发电的设想,并进行了实验研究,实验装置的示意图可用题23图表示,两块面积均为S的举行金属板,平行、正对、数值地全部浸在河水中,间距为d。水流速度处处相同,大小为v,方向水平,金属板与水流方向平行。地磁场磁感应强度的竖直分量为B,水的电阻率为p,水面上方有一阻值为R的电阻通过绝缘导线和电键K连接到两个金属板上,忽略边缘效应,求:
(1)该发电装置的电动势;
(2)通过电阻R的电流强度。
(3)电阻R消耗的电功率。
正确答案
见解析
解析
(1)由法拉第电磁感应定律,有E=Bdv
(2)两板间河水的电阻r=
由闭合电路欧姆定律,有
I=
(3)由电功率公式,P=I2R
得P=
知识点
为了降低潜艇噪音,提高其前进速度,可用电磁推进器替代螺旋桨。潜艇下方有左、右两组推进器,每组由6个相同的用绝缘材料制成的直线通道推进器构成,其原理示意图如下。在直线通道内充满电阻率ρ=0.2Ω∙m的海水,通道中a×b×c=0.3m×0.4m×0.3m的空间内,存在由超导线圈产生的匀强磁场,其磁感应强度B=6.4T、方向垂直通道侧面向外。磁场区域上、下方各有a×b=0.3m×0.4m的金属板M、N,当其与推进器专用直流电源相连后,在两板之间的海水中产生了从N到M,大小恒为I=1.0×103A的电流,设电流只存在于磁场区域。不计电源内阻及导线电阻,海水密度ρ≈1.0×103kg/m3。
(1)求一个直线通道推进器内磁场对通电海水的作用力大小,并判断其方向;
(2)在不改变潜艇结构的前提下,简述潜艇如何转弯?如何“倒车”?
(3)当潜艇以恒定速度v0=30m/s前进时,海水在出口处相对于推进器的速度v=34m/s,思考专用直流电源所提供的电功率如何分配,求出相应功率的大小。
正确答案
见解析。
解析
(1)安培力的大小,F=BIL=6.4×1000×0.3=1.92×103N,
根据左手定则可知,方向:垂直于BI平面向右;
(2)开启或关闭不同个数的左、右两侧的直线通道推进器,实施转弯。
改变电流方向,或改变磁场方向,可以改变海水所受磁场力的方向,实施“倒车”。
(3)电源提供的电功率中的第一部分为牵引功率
P1=F牵v0=6.9×105W
电源提供的电功率中的第二部分为单位时间内海水的焦耳热功率
推进器内海水的电阻
电源提供的电功率中的第三部分为单位时间内海水动能的增加量
单位时间内通过推进器的水的质量为
m=ρmbcv水对地=480kg
单位时间内其动能增加为P3=
知识点
如图(a)所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在辐射状电场和垂直纸面的匀强磁场,内外圆间的电势差U为常量,R1=R0,R2=3R0,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力。
(1)已知粒子从外圆上以速度v1射出,求粒子在A点的初速度v0的大小。
(2)若撤去电场,如图(b),已知粒子从OA延长线与外圆的交点C以速度v2射出,方向与OA延长线成45°角,求磁感应强度的大小及粒子在磁场中运动的时间。
(3)在图(b)中,若粒子从A点进入磁场,速度大小为v3,方向不确定,要使粒子一定能够从外圆射出,磁感应强度应小于多少?
正确答案
见解析。
解析
(1)根据动能定理, 
(2)如图所示,设粒子在磁场中作匀速圆周运




根据公式
解得:
(3)考虑临界情况,如图所示
①
②

知识点
空间有一圆柱形匀强磁场区域,该区域的横截面的半径为R,磁场方向垂直横截面。一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场,离开磁场时速度方向偏离入射方向60°。不计重力,该磁场的磁感应强度大小为
正确答案
解析
画出粒子的运动轨迹,由几何关系可知,粒子做圆周运动的半径


知识点
如图16(a)所示,左为某同学设想的粒子速度选择装置,由水平转轴及两个薄盘N1、N2构成,两盘面平行且与转轴垂直,相距为L,盘上各开一狭缝,两狭缝夹角
(1)若两狭缝平行且盘静止(如图16(c)),某一粒子进入磁场后,竖直向下打在感光板中心点M上,求该粒子在磁场中运动的时间t;
(2)若两狭缝夹角为θ0 ,盘匀速转动,转动方向如图16(b).要使穿过N1、N2的粒子均打到感光板P1P2连线上。试分析盘转动角速度
正确答案
(1)t =


解析
(1)粒子在磁场中匀速圆周运动,洛伦兹力提供向心力:
qBυ = 
周长=周期×速度,即:
2πR = υ T ....................................... ②
又有:t = 
解得:t =
(2)速度最小时有:
L = υ1t1 .......................................... ④
θ0 = ω1 t1 ...................................... ⑤
qBυ1 = 
求得:ω1 =
速度最大时有:
L = υ2t2 .......................................... ⑦
θ0 = ω2 t2 ...................................... ⑧
qBυ2 = 
R2 = (R−
解得:ω1 =
所以:
知识点
扫码查看完整答案与解析