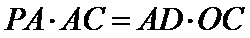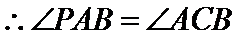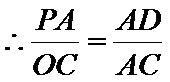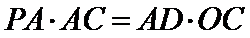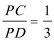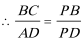- 相似三角形的性质
- 共11题
22.如图(8),圆O1与圆O2相交于A、B两点,AB是圆O2的直径,过A点作圆O1的切线交圆O2于点E,并与BO1的延长线交于点P,PB分别与圆O1、圆O2交于C,D两点.
(Ⅰ)求证:PA·PD=PE·PC;
(Ⅱ)求证:AD=AE.
正确答案
(1)见解析;(2)见解析
解析
试题分析:本题属于几何证明选讲中的证明问题,
(1)由切割线定理直接证明;(2)直接按照步骤来求。



又

由①,②得
(2)连接AC,DE, 
由(1)知,
AB是⊙O2的直径,
考查方向
解题思路
本题考查几何证明选讲中的证明问题,解题步骤如下:
(1)由切割线定理直接证明;
(2)直接按照步骤来求。
易错点
图形看不懂,比较复杂。
知识点
22. 如图,在








(Ⅰ)求证:
(Ⅱ)求线段
正确答案
(1)见解析;(2)
解析
试题分析:本题属于几何证明选讲的问题,
(1)由割线定理求解(2)由割线定理求解.
(Ⅰ)证明:由已知


(Ⅱ)解:如图,过点








即
所以
考查方向
解题思路
本题考查几何证明选讲的问题,解题步骤如下:
由割线定理求解。用割线定理来解决。
易错点
不会利用切割线定理来解答。
知识点
如图所示,直线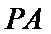
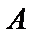
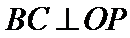

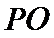
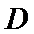
27.证明: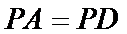
28.证明:
正确答案
见解析
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
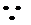
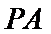
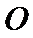
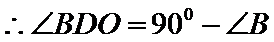
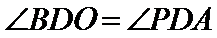
考查方向
解题思路
(1)利用切割线定理即可得证;
(2)利用三角形相似即可证明.
易错点
相关定理不熟悉导致本题失分。
正确答案
见证明.
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
连结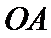
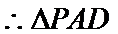

考查方向
解题思路
(1)利用切割线定理即可得证;
(2)利用三角形相似即可证明.
易错点
相关定理不熟悉导致本题失分。
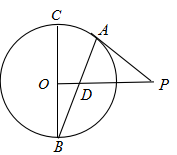
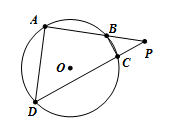
如图,










正确答案
4
解析
连接OC,BC,易知PB=OC=OB=r,由切割线定理知r=2,故AB=4.
知识点
选做题(14、15题,只能从中选做一题)
14.在同一平面坐标系中,经过伸缩变换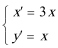
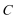
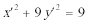
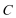
15.如图,四边形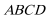
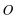
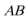
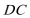
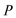
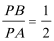
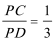
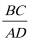
正确答案
14.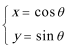
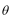
15.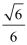
解析
14.将
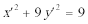
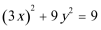
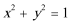
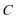
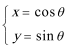
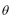
15.由于四边形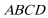
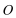
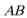
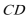
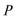
则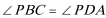
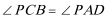
知识点
扫码查看完整答案与解析