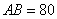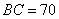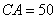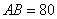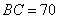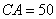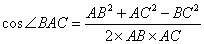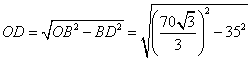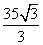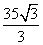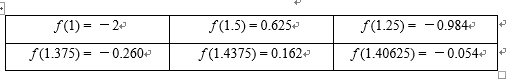- 函数模型的选择与应用
- 共38题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某商场2013年一月份到十二月份月销售额呈现先下降后上升的趋势,现有三种函数模型:
①



能较准确反映商场月销售额


正确答案
③,
解析
略
知识点
某市旅游部门开发一种旅游纪念品,每件产品的成本是





(1)写出

(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大。
正确答案
见解析。
解析
(1)改进工艺后,每件产品的销售价为


∴



(2)由


当



∴函数


故改进工艺后,产品的销售价为
知识点
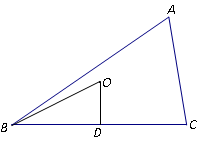
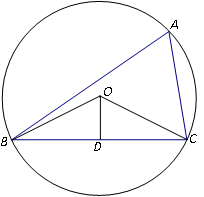
某单位有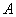
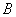
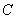
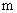
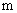
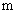
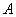
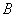
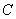
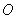
(1)求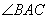
(2)求点
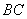
正确答案
见解析。
解析
(1)在△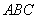
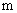
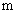
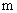
由余弦定理得
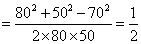
因为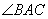
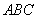
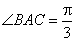
(2)
方法1:因为发射点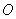
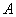
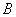
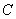
所以点
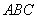
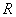
在△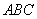
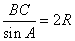
因为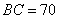
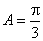
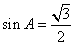
所以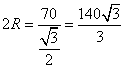
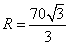
过点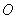
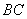
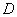
在△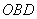
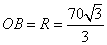
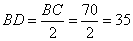
所以
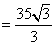
所以点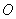
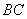
方法2:
因为发射点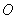
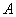
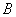
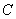
所以点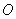
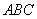
连结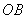
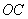
过点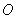
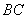
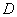
由(1)知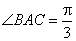
所以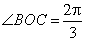
所以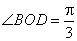
在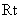
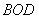
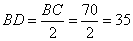
所以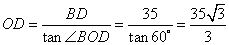
所以点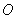
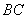
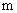
知识点
某公司一年购买某种货物





正确答案
30
解析
略
知识点
若函数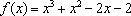
那么方程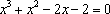
正确答案
解析
略
知识点
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施,该设施的下部ABCD是正方形,其中AB=2米;上部CDG是等边三角形,固定点E为AB的中点,△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆。
(1)设MN与AB之间的距离为
(2)求△EMN的面积S(平方米)的最大值。
正确答案
(1)
(2)最大值为2平方米
解析
解析:(1)
①如图1所示,当MN在正方形区域滑动,
即0<x≤2时,
△EMN的面积S=

②如图2所示,当MN在三角形区域滑动,
即2<x<
如图,连接EG,交CD于点F,交MN于点H,
∵ E为AB中点,


又∵ MN∥CD,
∴ △MNG∽△DCG。
∴ 

故△EMN的面积S=
=
综合可得:

说明:讨论的分段点x=2写在下半段也可。
(2)①当MN在正方形区域滑动时,

②当MN在三角形区域滑动时,S=
因而,当


所以当
知识点
如图,建立平面直角坐标系




(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标
正确答案
(1)10千米;(2)当
解析
(1)在


由实际意义和题设条件知
∴

∴炮的最大射程是10千米。
(2)∵


即关于

由

此时,
∴当
知识点
噪声污染已经成为影响人们身体健康和生活质量的严重问题. 实践证明,声音强度





(1)当声音强度






(2)当人们低声说话,声音能量为






正确答案
(1)

解析
(1)



(2)由题意得


答:当声音能量
知识点
21。某旅游景点预计2013年1月份起前x个月的旅游人数的和p(x)(单位:万人)与x的关系近似地满足
(1)写出2013年第x月的旅游人数
(2)试问2013年第几月旅游消费总额最大,最大月旅游消费总额为多少元?
正确答案
见解析。
解析
(1)当

当


验证

(2)第
即
当



解得








当




综上,2013年第5月份的旅游消费总额最大,最大消费总额为3125万元. …12分
知识点
扫码查看完整答案与解析