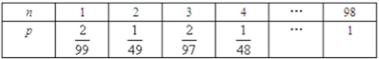- 函数模型的选择与应用
- 共38题
21.已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品

(1)写出年利润

(2)年产量为多少千件时,该企业生产此产品所获年利润最大?(注:年利润=年销售收入-年总成本)
正确答案
(1)当

当

(2)①当




当





②当

当且仅当


综合①、②知

所以为9千件时,该企业生产此产品获利最大.
解析
解析已在路上飞奔,马上就到!
知识点
20.近年来,某企业每年消耗电费约24万元, 为了节能减排





(1)试解释

(2)当
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.请你设计一个LED霓虹灯灯箱.现有一批LED霓虹灯灯箱材料如图所示,ABCD是边长为60 cm的正方形LED散片,边CD上有一以其中点M为圆心,半径为2 cm的半圆形缺损,因此切去阴影部分(含半圆形缺损)所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于空间一点P,正好形成一个正四棱柱形状有盖的LED霓虹灯灯箱,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE= FB=xcm.
(1)用规格长×宽×高=145 cm×145 cm ×75 cm外包装盒来装你所设计的LED霓虹灯灯箱,灯箱彼此间隔空隙至多0.5 cm,请问包装盒至少能装多少只LED霓虹灯灯箱(每只灯箱容积V最大时所装灯箱只数最少)?
(2)若材料成本2元/


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知农民收入由工资性收入和其他收入两部分构成.2005年某地区农民人均收入为3150元(其中工资性收入为1800元,其他收入为1350元),预计该地区自2006年起的5年内,农民的工资性收入将以6 %的年增长率增长,其他收入每年增加160元。根据以上数据,2010年该地区农民人均收入介于 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某工厂统计资料显示,产品次品率p与日产量n(件)(n∈N*,且1≤n≤98)的关系表如下:又知每生产一件正品盈利a元,每生产一件次品损失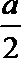
(1)将该厂日盈利额T(元)表示为日产量n(件)的一种函数关系式;
(2)为了获得最大盈利,该厂的日产量应定为多少件?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析