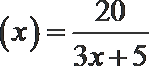- 函数模型的选择与应用
- 共38题
20.我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年,每厘米厚的隔热层建造成本是3万元,天宫一号每年的能源消耗费用C(万元)与隔热层厚度

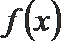
(1)求
(2)当隔热层修建多少厘米厚时,总费用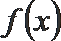
正确答案
(1)当
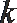
(2)
当且仅当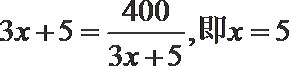
即隔热层修建5厘米厚时,总费用达到最小值,最小值为35万元.
解析
解析已在路上飞奔,马上就到!
知识点
21. 国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费,每一年度申请总额不超过6000元。某大学2010届毕业生王某在本科期间共申请了


签约的单位提供的工资标准为第一年内每月







(Ⅰ)用



(Ⅱ)若王某恰好在第36个月(即毕业后三年)还清贷款,求
(Ⅲ)当

(参考数据:
正确答案
(Ⅰ)
(Ⅱ)依题意,从第13个月开始,每个月的还款额为



令

即要使在三年全部还清,第13个月起每个月必须比上一个月多还
(Ⅲ)设王某第
整理可得


即王某工作
这个月王某的还款额为

第32个月王某的工资为
因此,王某的剩余工资为
解析
解析已在路上飞奔,马上就到!
知识点
20.围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),
其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
正确答案
(Ⅰ)如图,设矩形的另一边长为a m,
则
由已知xa=360,得a=
(II)


即当x=24m时,修建围墙的总费用最小,最小总费用是10440元。
解析
解析已在路上飞奔,马上就到!
知识点
18. 为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为

(1)y关于x的函数解析式y=f(x);
(2)若BC的长不得超过40m,则当BC为何值时,y有最小值,并求出这个最小值。
正确答案
解:(1)
(2)令
因为

所以
故当x=40m时,y取理最小值225m
解析
解析已在路上飞奔,马上就到!
知识点
20.为了提高产品的年产量,某企业拟在2014年进行技术改革,经调查测算,产品当年的产量




(1)试确定


(2)该企业2014年的技术改革费用投入多少万元时,厂家的利润最大?并求出最大利润.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析