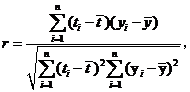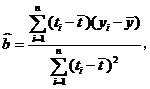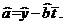- 回归分析
- 共4题
18.
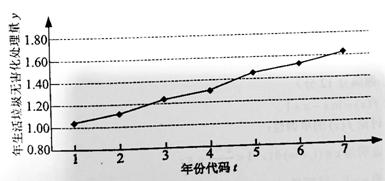
下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图。
注：年份代码1~7分别对应年份2008~2014.
（Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；
（Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.
附注：
参考数据：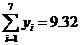
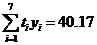
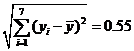
参考公式：
回归方程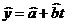
正确答案
（Ⅰ）由折线图中数据和附注中参考数据得
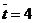
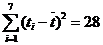
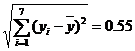
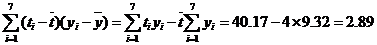
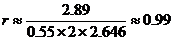
因为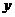
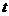
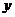
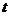
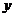
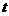
（Ⅱ）由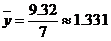
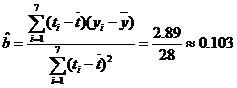
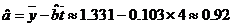
所以，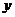
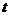
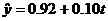
将2016年对应的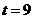
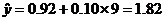
所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨. .........12分
知识点
5．某产品的广告费用x与销售额y的统计数据如下表所
正确答案
解析
由表中数据得：
从而线性回归方程为
考查方向
解题思路
根据回归直线方程过样本的中心点即可解出。
易错点
不知道考查的知识点是什么。
知识点
随着我国经济的发展，居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款（年底余额）如下表：
（本小题满分13分，（Ⅰ）小问10分，（Ⅱ）小问3分）
18.求y关于t的回归方程
19.用所求回归方程预测该地区2015年（
附：回归方程
正确答案
（Ⅰ）
解析
试题分析：（Ⅰ）列表分别计算出
试题解析： （1）列表计算如下
这里
又
从而
故所求回归方程为
考查方向
解题思路
本题考查线性回归直线方程的求法及应用，采用列表方式分别求出
易错点
准确运用公式求解有关量.
正确答案
（Ⅱ）
解析
试题分析： （Ⅱ）将
试题解析：（2）将
考查方向
解题思路
本题考查线性回归直线方程的应用，代入数据求解即可.
易错点
注意运算的准确性.
11.某学校开展研究性学习活动，某同学获得一组实验数据如下表：
对于表中数据,现给出以下拟合曲线,其中拟合程度最好的是（ ）
Ay＝2x－2
By＝
Cy＝log2x
Dy＝
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析