热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

16. 已知函数

（I）求函数的单调递减区间；

（II）在中，分别是角A、B、C的对边，，求边长c的值.

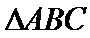
正确答案

见解析

解析

考查方向

本题主要考察了二倍角的余弦公式，考察了两角和与差的正弦公式，考察了三角函数的恒等变换及化简求值，考察了余弦定理，余弦定理的应用，均值定理，考察了向量的数量积运算

解题思路

该题解题思路如下

1）使用和角公式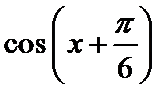展开

2）利用倍角公式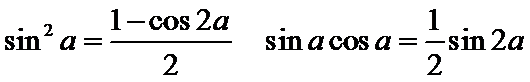对解析式降次

3）使用辅助角公式对解析式化简

4）利用特殊角的三角函数求值得到角C，

5）使用余弦定理得到a，b的关系，使用余弦定理求c

易错点

该题易于忽略了对C的范围的判断，该题属于简单

知识点

正弦函数的单调性三角形中的几何计算

题型：单选题

单选题 · 5 分

12．若函数在(-∞,+∞)单调递增，则a的取值范围是( )

A[-1,1]

B[-1,]

C[-,]

D[-1,-]

正确答案

知识点

正弦函数的单调性三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

10.已知函数（，，）的部分图象如图所示，则的递增区间为（）

A，

B，

C，

D，

正确答案

解析

由图象可知，A=2,,所以,所以,因此，f(x)的单调增区间为

考查方向

三角函数的图象的性质和特征

解题思路

根据所给图象求出未知参数，进而得到函数的递增区间

易错点

计算错误，对三角函数的图象性质掌握不好

知识点

正弦函数的单调性

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 正弦函数的对称性

百度题库 > 高考 > 文科数学 > 正弦函数的单调性

扫码查看完整答案与解析