- 函数的概念及其构成要素
- 共1288题
已知函数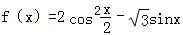
(1)求函数f(x)的最小正周期和值域;
(2)若a为第二象限角,且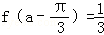
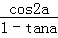
正确答案
见解析。
解析
(1)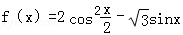
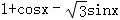
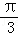
∴函数f(x)的周期为2π,
∵2cos(x+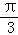
(2)因为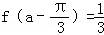
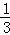
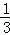
因为α为第二象限角,所以sinα=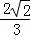
所以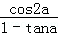
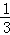
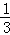
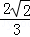
知识点
已知向量


(1)求函数
(2)已知





正确答案
见解析
解析
(1)由条件得



(2)由






知识点
已知函数

(1)设


(2)求函数
正确答案
见解析
解析
(1)由题设知
因为





所以
(2)

当


函数
故函数


知识点
设函数



(1)若随机数
(2)已知随机函数





正确答案
见解析。
解析
由


(1)因为随机数


列举如下:


事件A :



所以

(2)由题意,




事件A :
其面积为:
所以
即事件

知识点
设函数
(1) 求

(2)已知







正确答案
见解析。
解析
(1)


∴最小正周期
(2)由(1)知
当

∴当

∴

由余弦定理,得:
知识点
扫码查看完整答案与解析