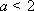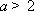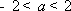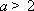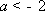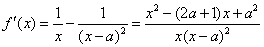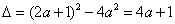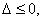- 函数的概念及其构成要素
- 共1288题
函数

正确答案
解析
略
知识点
设某商品的需求函数为






正确答案
解析
略
知识点
已知函数
(1)当


(2)讨论函数
正确答案
见解析
解析
函数


(1) 当


所以曲线


(2)
(i)当



(ii)当



当


此时,


(iii)当



当


此时,


知识点
已知函数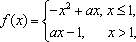
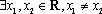
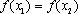

正确答案
解析
略
知识点
已知函数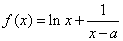
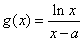
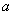
(1)求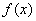
(2)若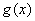
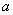
正确答案
见解析。
解析
(1)
设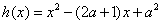
①当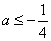
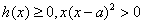
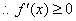
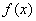
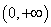
当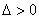
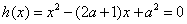
②当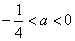
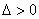
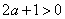
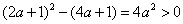
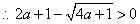
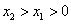
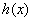
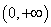
在区间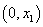
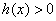
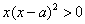
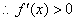
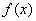
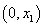
在区间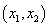
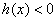
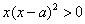
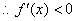
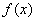
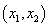
在区间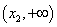
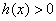
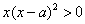
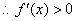
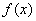
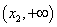
③当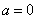
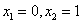
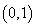
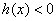
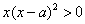
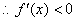
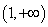
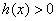
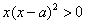
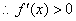
④当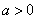
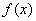
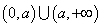
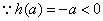
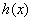
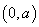
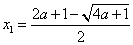
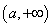
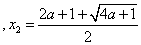
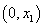
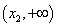
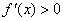
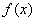
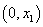
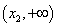
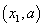
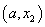
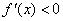
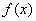
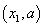
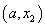
综上: 当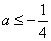
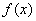
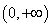
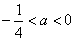
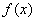
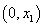
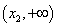
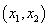
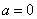
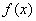
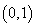
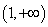
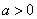
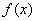
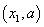
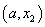
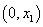
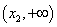
⑵当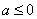
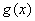
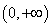
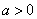
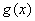
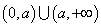
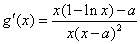
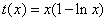
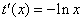
在区间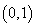
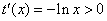
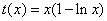
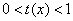
在区间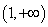
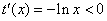
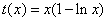
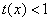
当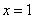
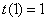
故当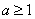
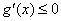
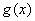
当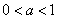
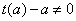
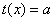
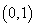
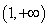
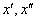
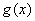
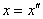
当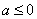
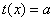
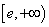
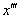
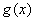
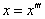
综上所述,若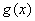
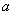
知识点
扫码查看完整答案与解析