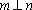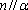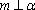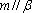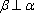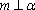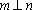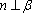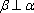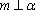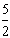- 直线与平面平行的判定与性质
- 共228题
如图,在直三棱柱
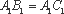

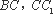


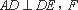

求证:(1)平面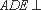
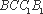
(2)直线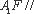

正确答案
见解析
解析
(1)∵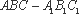

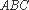
又∵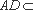
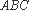
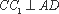
又∵
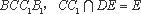
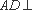
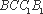
又∵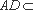
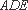
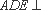
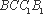
(2)∵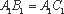
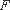
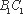
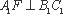
又∵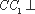
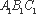
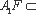
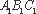
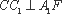
又∵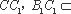

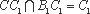
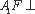
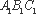
由(1)知,
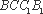
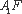
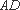
又∵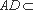
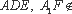
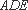

知识点
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=λAA′,点M,N分别为A′B和B′C′的中点。
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′-MNC的体积。
(锥体体积公式V=
正确答案
见解析
解析
(1)证法一:连结AB′,AC′,由已知∠BAC=90°,AB=AC,三棱柱ABC-A′B′C′为直三棱柱,
所以M为AB′中点。
又因为N为B′C′的中点,
所以MN∥AC′。
又MN

因此MN∥平面A′ACC′。
证法二:取A′B′中点P,连结MP,NP,
而M,N分别为AB′与B′C′的中点,
所以MP∥AA′,PN∥A′C′,
所以MP∥平面A′ACC′,
PN∥平面A′ACC′。
又MP∩NP=P,
因此平面MPN∥平面A′ACC′。
而MN
因此MN∥平面A′ACC′。
(2) (2)解法一:连结BN,由题意A′N⊥B′C′,平面A′B′C′∩平面B′BCC′=B′C′,所以A′N⊥平面NBC。
又A′N=
故VA′-MNC=VN-A′MC=


解法二:VA′-MNC=VA′-NBC-VM-NBC=
知识点
设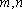
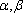
正确答案
解析
对A,若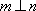
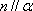

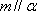
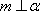
对B,若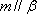
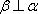

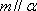

对C,若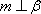
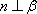
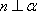
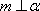
对D,若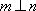
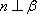
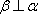
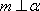

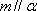
故选C. 点评:本题考查空间中的线线、线面、面面的闻之关系,容易题
知识点
关于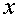
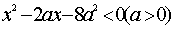
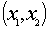
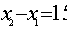
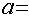
正确答案
解析
∵由x2-2ax-8a2<0(a>0),得(x-4a)(x+2a)<0,即-2a<x<4a,∴x1=-2a,x2=4a.
∵x2-x1=4a-(-2a)=6a=15,
∴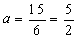
知识点
设





正确答案
解析
知识点
扫码查看完整答案与解析