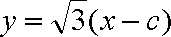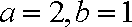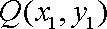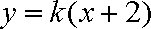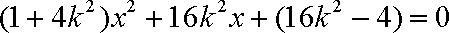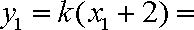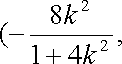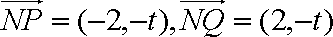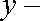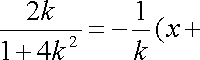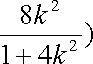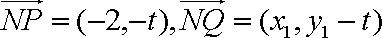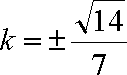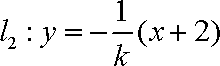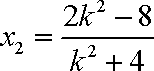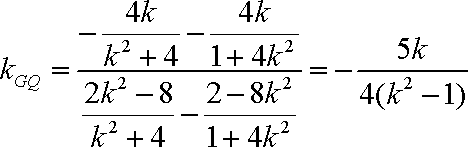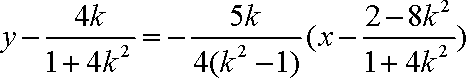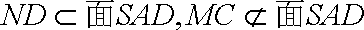- 直线与平面平行的判定与性质
- 共228题
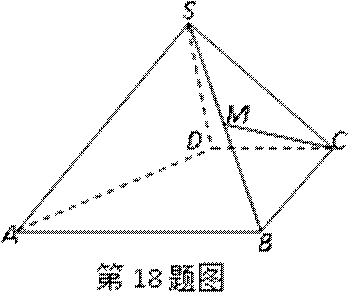
如图,在六面体



(1)
(2)
正确答案
见解析
解析
证明:(1)取线段



因为

所以

又




而

所以
(2)因为




所以

又



所以

所以
知识点
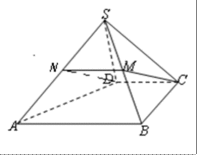
如图,四棱锥







(1)证明:
(2)证明:

正确答案
见解析。
解析
证明:
(1)由



又

(2)
取




又


所以

知识点
设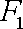
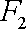

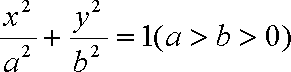
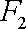


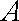
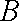
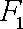
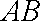


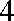
(1)求椭圆
(2)过椭圆
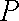
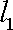

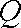
(ⅰ)若点

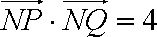
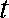
(ⅱ)过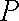
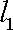
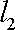


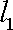
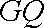

正确答案
见解析。
解析
(1)设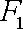
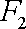
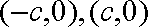
由题意得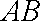
因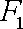
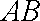

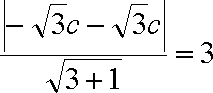
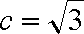
所以有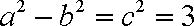
由题意知: 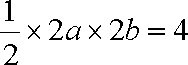
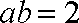
联立①②解得:
所求椭圆
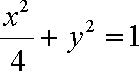
(2)由(1)知: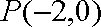
根据题意可知直线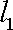
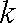
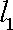
把它代入椭圆
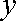
由韦达定理得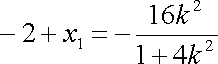
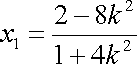
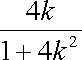
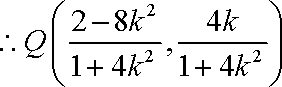

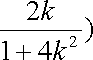
(ⅰ)当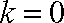
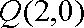

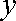
于是
由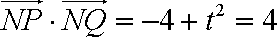
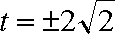
当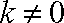

因为点

令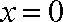
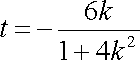
由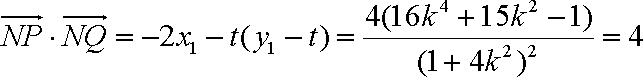
代入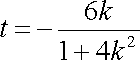
综上, 满足条件的实数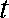
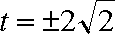
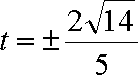
(ⅱ)设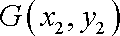
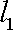
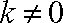
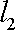
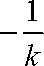
由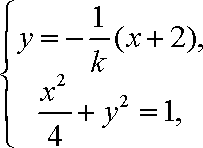
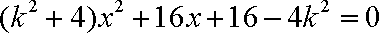
∵此方程有一根为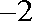
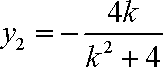
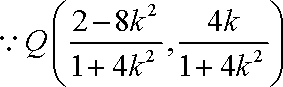
所以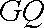
令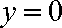
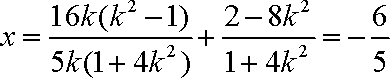
所以直线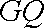

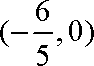
知识点
设正四棱锥的侧棱长为1,则其体积的最大值为 。
正确答案

解析
法1 设正四棱锥的底面边长为






法2 设正四棱锥的侧棱与底面所成角为






知识点
如图,四棱锥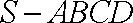
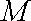
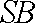
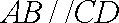


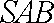
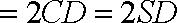
(1)证明:
(2)证明: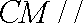
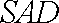
正确答案
见解析。
解析
(1)由
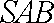
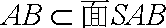

又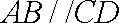

(2)
取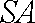
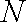
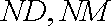
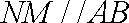
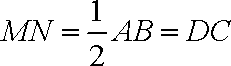
又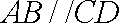
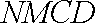
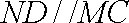
所以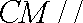
知识点
扫码查看完整答案与解析