- 奇偶性与单调性的综合
- 共14题
1
题型:填空题
|
15.已知函数
① 函数
② 函数

③ 函数

④ 对任意两个不相等的实数

其中所有真命题的序号是 .
正确答案
①③
解析
因为
且
所以函数











考查方向
本题主要考查了函数的对称性、单调性、周期性等性质.
解题思路
1)利用

2)由对称性判定其他性质.
易错点
本题易在判定函数的对称性时出现错误,易忽视“若


知识点
奇偶性与单调性的综合函数性质的综合应用
1
题型:
单选题
|
11. 定义在R上的函数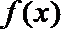
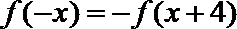
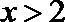
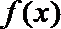
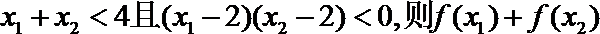
正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
奇偶性与单调性的综合
1
题型:填空题
|
8.若f(x)是奇函数,且在(-∞,0)上是增函数,又f(-2)=0,则满足xf(x-1)>0的x取值范围为_________.
正确答案
解析
画一个草图,
由xf(x-1)>0⇒
或
即x的取值范围为{x|x<-1或0<x<1或x>3}.
知识点
奇偶性与单调性的综合抽象函数及其应用其它不等式的解法
1
题型:填空题
|
16. 定义在




②

③

④

则正确命题的序号为 .
正确答案
②③
解析
①因为

②


③因为





④判断不出单调性,所以④不对。
考查方向
本题主要考察了函数的单调性、对称性以及奇偶性,在近几年的高考中经常涉及,难度偏大。
解题思路
(1)由










易错点
不会利用已知条件求函数的周期,不会判断函数的对称性
知识点
命题的真假判断与应用奇偶性与单调性的综合
下一知识点 : 函数的图象
扫码查看完整答案与解析



