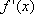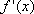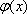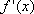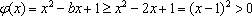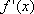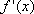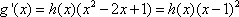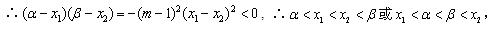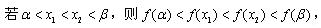- 导数及其应用
- 共3028题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
曲线

正确答案
解析
求导得



知识点
已知函数
(1)若曲线

(2)设函数


(3)对(2)中的

正确答案
见解析。
解析
(1)
由已知得

∴ 两条直线交点的坐标为

∴ 切线的方程为
(2)由条件知
∴
(ⅰ)当a>0时,令

∴ 当


当


∴



∴最小值
(ⅱ)当


故

(3)由(2)知
对任意的



故由①②③得
知识点
过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,O为坐标原点,若|AF|=3,则△AOB的面积为( )
正确答案
解析
设∠AFx=θ(0<θ<π)及|BF|=m,
∵|AF|=3,
∴点A到准线l:x=﹣1的距离为3
∴2+3cosθ=3
∴cosθ=
∵m=2+mcos(π﹣θ)
∴
∴△AOB的面积为S=
知识点
设


(1)求集合
(2) 求函数

正确答案
(1)
(2) 当




解析
(1)由方程
因为
当



当



当




则 

当


此时,
当

此时,
综上,
(2) 
所以函数



当




当




当
由
(可以用作差法,也可以用分析法),所以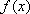


当
由


综上,当




知识点
过抛物线








正确答案
2
解析





故由面积可得:
知识点
已知函数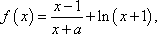
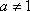
(1)若a=-2,求曲线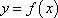
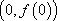
(2)若
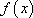
正确答案
见解析。
解析
知识点
设函数
(1)当a=1时,求
(2)若


正确答案
见解析。
解析
对函数求导得:
(1)单调性的处理,通过导数的零点进行穿线判别符号完成。
当a=1时,令
当

(2)区间
待定量a的值。
当

最大值在右端点取到。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
函数y=x2(x>0)的图像在点(ak,ak2)处的切线与x轴交点的横坐标为ak+1,k为正整数,a1=16,则a1+a3+a5=____▲_____
正确答案
21
解析
考查函数的切线方程、数列的通项。
在点(ak,ak2)处的切线方程为:


所以
知识点
设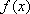
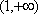
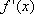

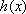

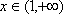
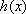
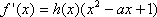
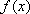
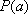
(1)设函数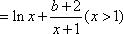

(i)求证:函数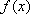
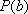
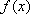
(2)已知函数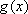
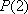
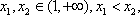
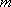
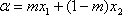
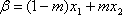

若|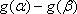
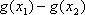
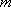
正确答案
见解析。
解析
(1)(i)
∵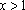
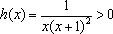
∴函数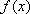
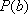
(ii)(方法一)设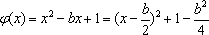
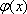
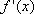
当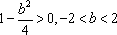
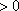
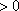
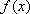
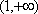
当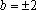
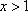
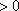
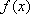
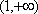
当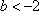
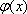

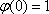
对于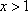
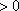
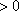
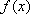
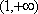
(方法二)当
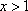
所以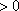
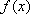
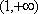
当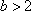
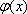
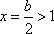
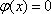
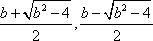
当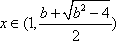
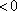
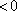
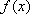
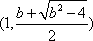
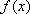

综上所述,当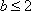
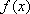
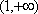
当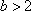
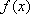
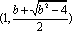
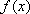
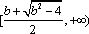
(2)(方法一)由题意,得:
又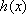
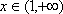

所以对任意的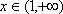
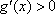
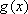
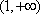
又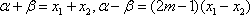
当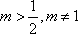
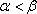
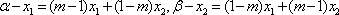
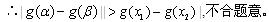
综合以上讨论,得:所求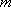
(方法二)由题设知,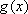
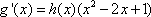
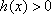
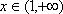
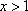
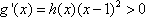
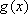
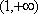
①当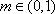
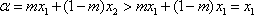
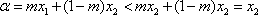
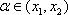
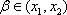
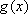
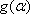
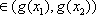
从而有|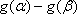
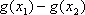
②当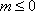
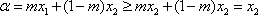
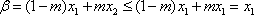
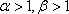
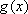
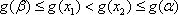
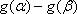
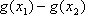
③当
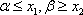
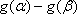
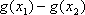
因此综合①、②、③得所求的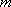
知识点
已知函数

(1)若对一切


(2)在函数






正确答案
见解析
解析
(1)若



故
而
当





于是对一切

令
当



故当




综上所述,

(2)由题意知,
令
令

当



故当

从而

所以
因为函数








综上所述,存在



知识点
扫码查看完整答案与解析