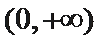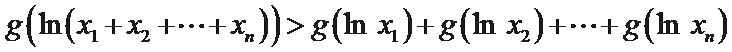- 导数及其应用
- 共3028题
10.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)求证:
(2)当




正确答案
(1)
依题意

(2)






即
考虑函数



所以



由




解析
解析已在路上飞奔,马上就到!
知识点
5. 若f(x)=x2 -2x-4lnx,则f′(x)>0的解集为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数

正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
11.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 张家界某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值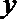
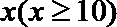
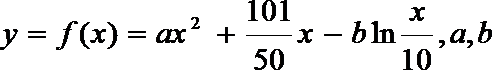
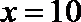
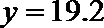
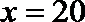
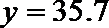
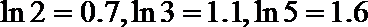
(1)求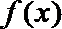
(2)求该景点改造升级后旅游利润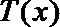
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数




(Ⅰ)求a的值;
(Ⅱ)是否存在k的值,使直线
(Ⅲ)如果对于所有

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.对于函数f(x)(x∈D),若x∈D时,恒有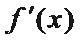
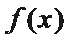
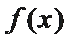
(Ⅰ)当函数f(x)=m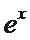
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,试比较g(a)与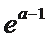
正确答案
解:(Ⅰ)由
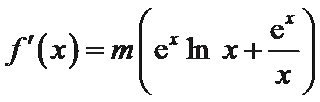
因为函数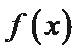
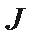
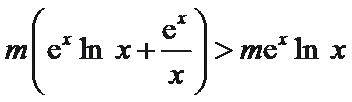
即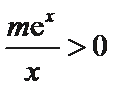
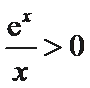
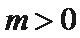
即
(Ⅱ)①构造函数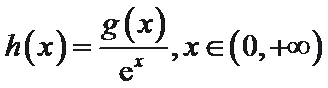
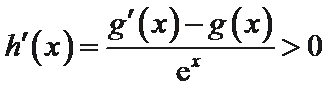
可得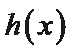
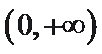
当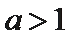
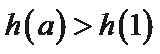
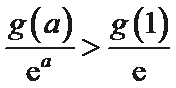
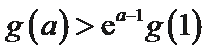
当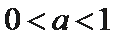
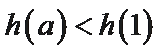
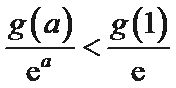
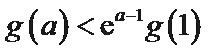
当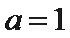
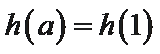
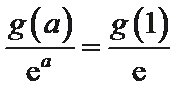
②因为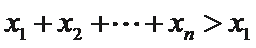
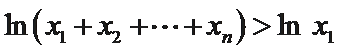
由①可知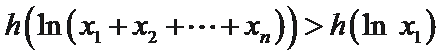

整理得
同理可得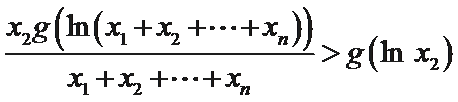
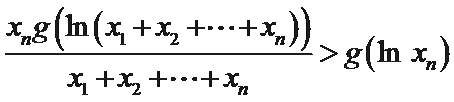
把上面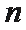
可得
解析
解析已在路上飞奔,马上就到!
知识点
21. 设函数




(Ⅰ)求

(Ⅱ)证明:当

(Ⅲ)若当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知R上的连续函数g(x)满足:
①当



②对任意的






若关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.给出以下四个命题:
①命题



②求函数
③函数





④函数
其中不正确的命题序号是__________(把你认为不正确的命题序号都填上).
正确答案
②
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析