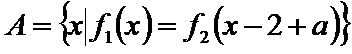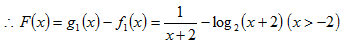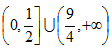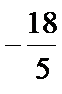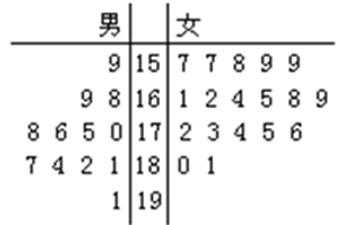- 导数及其应用
- 共3028题
19.如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=900,O为BC中点;
(Ⅰ)证明:SO⊥平面ABC;
(Ⅱ)求二面角A-SC-B的余弦值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数f(x)的定义域为R,若存在常数M>0使
①f(x)=x2
②f(x)=
③f(x)=x(1-2x)
④f(x)是定义在实数集R上的奇函数,且对一切x1x2均有
其中是F函数的序号为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数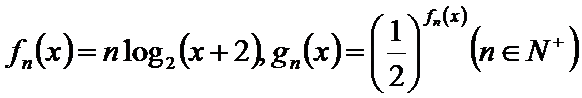
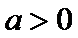
(1)确定实数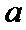
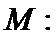
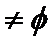
(2)确定实数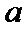
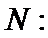
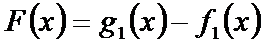
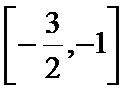
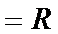
(3)如果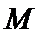
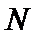

正确答案
(1)方程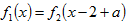
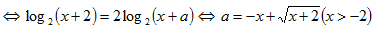
令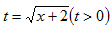
则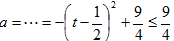
故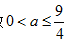
(2)又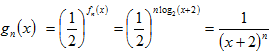
由于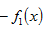
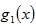
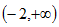
故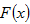
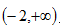
而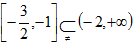
故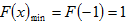
依题意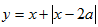
而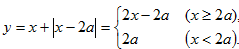
则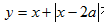
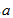
因此,若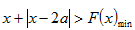
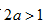
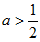
(3)如果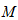
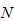
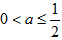
如果


故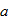
解析
解析已在路上飞奔,马上就到!
知识点
8.已知关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图









(1)如图甲,要建的活动场地为△
(2)如图乙,要建的活动场地为等腰梯形
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元,用η表示经销一辆汽车的利润。
(Ⅰ)求上表中的a,b值;
(Ⅱ)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3
(Ⅲ)求η的分布列及数学期望Eη。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知

(Ⅰ)求c的值;
(Ⅱ)在函数

(Ⅲ)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 以下命题:
①若


② 


③若△


④若非零向量



⑤已知△ABC中,

其中所有真命题的序号是( )。
正确答案
①②④⑤
解析
解析已在路上飞奔,马上就到!
知识点
10.已知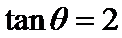

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
18. 第4届湘台经贸洽谈交流会于2011年6月在我市举行 ,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如下所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”, 身高在175cm以下(不包括175cm)定义为“ 非高个子 ”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用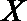
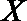
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 设函数




(i)
(ii)若关于


正确答案
0.15;
解析
解析已在路上飞奔,马上就到!
知识点
3. 在平面直角坐标系中,若角




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 用反证法证明命题:“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 如图,曲线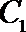
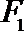
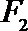
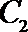
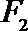
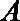
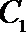
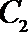
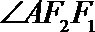
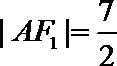
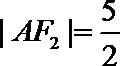
(Ⅰ)求曲线
(Ⅱ)过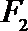

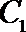
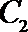
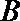
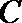
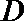
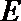
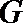
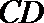

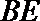
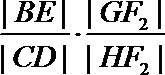
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析