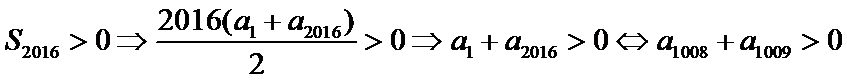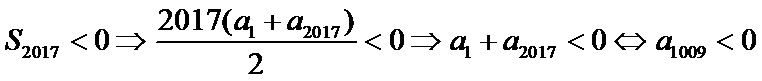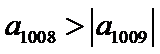- 数列与不等式的综合
- 共132题
9.设等差数列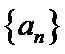
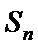
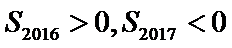
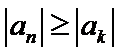
正确答案
解析
∵
故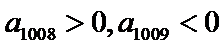
∴对任意正整数n,都有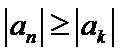
考查方向
解题思路
由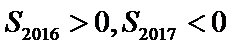
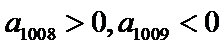
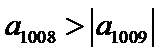
易错点
本题不易在利用前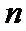
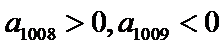
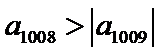
知识点
已知{

17.求数列{

18.若-

正确答案
(1)
解析
解:(Ⅰ)由题意,
代入得




所以
考查方向
解题思路
(1)通过等差等比数列的定义求出d和q,(2)先求出
易错点
寻找
正确答案
(2)
解析
解:
(Ⅱ)记
所以

所以

所以
考查方向
解题思路
(1)通过等差等比数列的定义求出d和q,(2)先求出
易错点
寻找
在等差数列








17.求

18.证明:
正确答案
见解析
解析
设








考查方向
解题思路
第一问根据前N项和求通项公式,第二问用裂项相消的办法证明不等式
易错点
相关性质掌握不好;不会求数列的和
正确答案
见解析
解析
因为





所以

考查方向
解题思路
第一问根据前N项和求通项公式,第二问用裂项相消的办法证明不等式
易错点
相关性质掌握不好;不会求数列的和
设数列



16.求数列
17.记数列


正确答案
解析
由已知

即
从而
又因为

所以

所以,数列
故
考查方向
解题思路
利用





易错点
不会根据Sn=2an-a3求出an=2an-1(n≥2);
正确答案
10.
解析
由(1)得
所以
由

因为
所以
于是,使
考查方向
解题思路
由(1)得



易错点
求前n项和时对于项数出错。
已知数列








24.比较


25.证明:

正确答案
解析
由

两式相减得:

又

∴

即:
考查方向
解题思路
先由通项及数列的前n项和的关系,求出通项,再求和,进而得出数列
易错点
在利用数列的前n项和与通项的关系时,易忽略对首项的验证
正确答案
略
解析
解:由(Ⅰ)知:

因此当

则
----------------------------------11分
又∵当

当且仅当
∴
∴

考查方向
解题思路
逐级对数列{






易错点
在构造数列放缩时,放缩不合理,导致出错
若等差数列


17.求
18.设数列



正确答案
a=3;
解析
设等差数列


即


解得
考查方向
解题思路
将原式变形


易错点
前n项和与通项的转化
正确答案
见解析
解析
由(1)
考查方向
解题思路
将原式变形


易错点
裂项求和应用不熟练.
(本小题满分12分,(1)小问4分,(2)小问8分)
在数列
27.若

28.若
正确答案

解析
试题分析:(1)由于






试题解析:(1)由
若存在某个






从而


故
考查方向
解题思路
数列的问题难度大,往往表现在与递推数列有关,递推含义趋广,不仅有数列前后项的递推,更有关联数列的递推,更甚的是数列间的“复制”式递推;从递推形式上看,既有常规的线性递推,还有分式、三角、分段、积(幂)等形式.在考查通性通法的同时,突出考查思维能力、代数推理能力、分析问题解决问题的能力.
易错点
本题第(1)小题通过递推式证明数列是等比数列,从而应用等比数列的通项公式求得通项.
正确答案
证明详见解析
解析
试题分析:(2)本小题是数列与不等式的综合性问题,数列的递推关系是









试题解析:(2)由



由上式及
因为
求和得
另一方面,由上已证的不等式知
综上:
考查方向
解题思路
数列的问题难度大,往往表现在与递推数列有关,递推含义趋广,不仅有数列前后项的递推,更有关联数列的递推,更甚的是数列间的“复制”式递推;从递推形式上看,既有常规的线性递推,还有分式、三角、分段、积(幂)等形式.在考查通性通法的同时,突出考查思维能力、代数推理能力、分析问题解决问题的能力.
易错点
第(2)小题把数列与不等式结合起来,利用数列的递推式证明数列是单调数列,利用放缩法证明不等式,难度很大.
已知正项数列




22.求

23.是否存在非零整数
对一切

正确答案

解析
解:由.
当



当
由
∵


∴

另法:易得



考查方向
解题思路
利用数列前


另法:易得



易错点
利用数列前


正确答案
存在
解析
由

设


∵


假设存在这样的实数


① 当

② 当


综上,


考查方向
解题思路
先进行化简转化




易错点
利用数列前


已知数列

24.若

25.若



正确答案
见解析
解析
(1)
当
当
考查方向
解题思路
由数列

易错点
主要易错于递推关系找不出,
正确答案
见解析
解析
(2)方法1:

①/②得,因为
方法2:因为
又因为
所以

所以

所以:
考查方向
解题思路
这里可以从两个方面进行分析
①直接找出
②根据递推关系得出
易错点
主要易错于递推关系找不出,
21.(本题满分15分)
已知数列






(1)证明:1

(2)设数列



正确答案
(1)详见解析;(2)详见解析;
解析
试题分析:(1)首先根据递推公式可得





(1)由题意得,







(2)由题意得






考查方向
解题思路
(1)根据题意,首先求出

易错点
对数列的通项公式要灵活变形.
知识点
扫码查看完整答案与解析