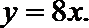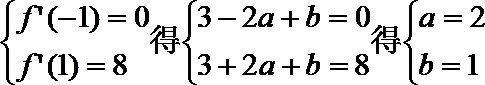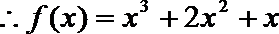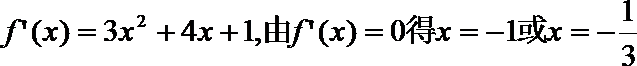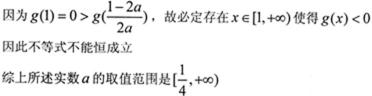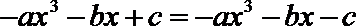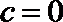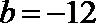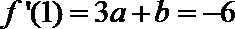- 导数及其应用
- 共2569题
13. 曲线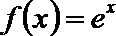

正确答案
x – y + 1= 0
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)若


(2)若在区间


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数


(I)求函数
(II)若对于区间



(III)若过点


正确答案
(I)

即

(II)令


则对于区间[-2,2]上任意两个自变量的值

所以

(Ⅲ)设切点为




因为过点

所以方程
即函数
则


解析
解析已在路上飞奔,马上就到!
知识点
22.函数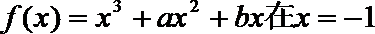
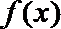

的切线平行于直线
(I)求函数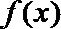
(II)对任意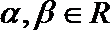

正确答案
解:(I)由
则
(II)
由(I)知
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知



(I)当


(II)求函数

(III)若在区间



正确答案
由

(I)当

所以

(II)令
(1) 当

故


(2)当


所以

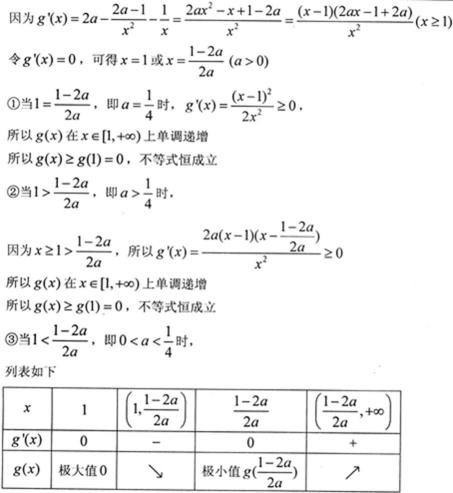
(III)设
对

因为





依题意,只需

即

所以正实数

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(Ⅰ)求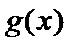
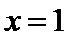
(Ⅱ)求
(Ⅲ)若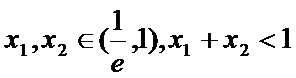
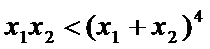
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.曲线

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
14.若抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数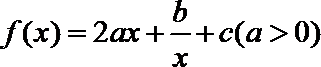

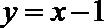
(1)用a表示出b,c;
(2)若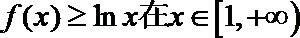
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知定义在正实数集上的函数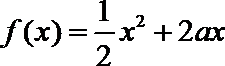
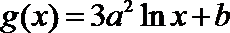
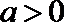
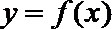
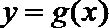
(I)用
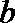
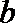
(II)求证: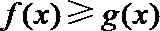
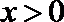
正确答案
(Ⅰ)设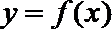
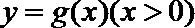
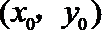
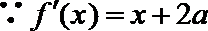
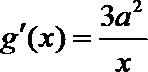
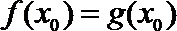
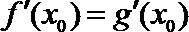
即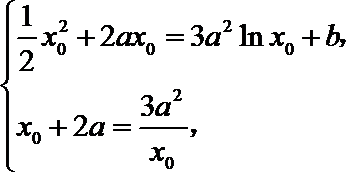
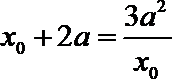
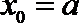
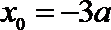
即有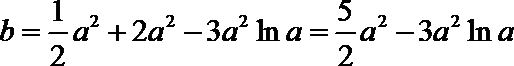
令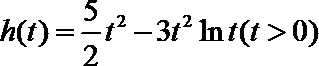
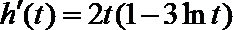
当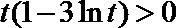
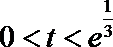
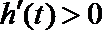
当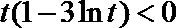
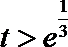
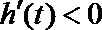
故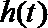
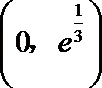
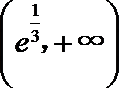
于是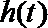
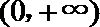
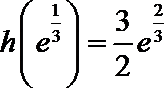
(Ⅱ)设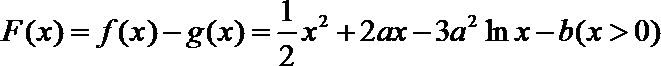
则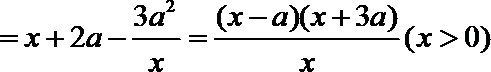
故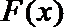
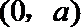
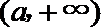
于是函数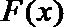
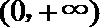
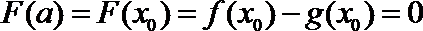
故当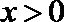
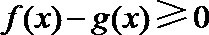
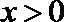
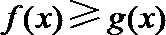
解析
解析已在路上飞奔,马上就到!
知识点
13.若曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设函数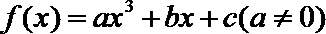
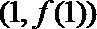
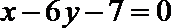
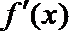
(1)求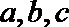
(2)求函数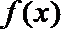
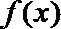
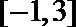
正确答案
(1)∵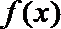
∴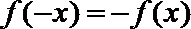
∴
∵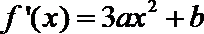
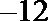
又直线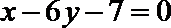

∴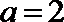
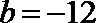
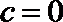
(2)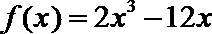
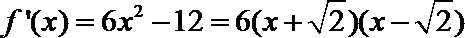
所以函数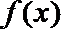
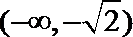
∵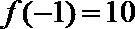
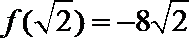
∴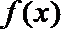
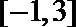
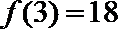
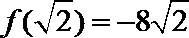
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数

(1)求函数
(2)若直线


(3)设



正确答案
解:(1)

在区间




所以,



(2)设切点坐标为
则
解得

(3)
则
解

所以,在区间

在区间

当



所以

当



所以

当



综上所述,当


当



当


解析
解析已在路上飞奔,马上就到!
知识点
18.


(1)求

(2)求切点坐标,求直线
正确答案
(1)k=-3
(2)设切点为
切线的斜率
代入到

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析