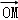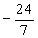- 三角函数与三角恒等变换
- 共2566题
已知点E、F分别在正方体ABCD-A1B1C1D1的棱BB1、CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC所成的二面角的正切值等于________。
正确答案
解析
法一:在平面BC1内延长FE与CB相交于G,过B作BH垂直AG,则EH⊥AG,故
∠BHE是平面AEF与平面ABC所成二面角的平面角,设正方体的棱长为a,可得
法二:设正方体的边长为3,建立以B1A1为x轴,B1C1为y轴,B1B为z轴的空间直角坐标系,则A(3,0,3),E(0,0,2),F(0,3,1),则=(3,0,1),=(0,3,-1),设平面AFE的法向量为n=(x,y,z),则n⊥,n⊥,即3x+z=0且3y-z=0,取z=3,则x=-1,y=1,所以n=(-1,1,3),又平面ABC的法向量为m=(0,0,3),所以面AEF
知识点
设常数a>0.若9x+


正确答案
[
解析
由题知,当x>0时,f(x)=9x+





知识点
在△ABC中,若
正确答案
解析
略
知识点
在△







(1)求角
(2)若

正确答案
(1)
(2)
解析
(1)因为
由正弦定理可得
因为在△

所以
又
所以
(2)由余弦定理 
因为

所以
因为
所以
当且仅当


知识点
已知△ABC的内角A,B及其对边a,b满足a+b=acotA+bcotB,求内角C.
正确答案
见解析。
解析
由


从而 

又
故

所以 
知识点
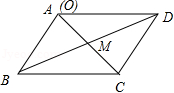
设M为平行四边形ABCD对角线的交点,O为平行四边形ABCD所在平面内任意一点,则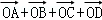
正确答案
解析
∵O为任意一点,不妨把A点看成O点,则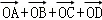
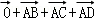
∵M是平行四边形ABCD的对角线的交点,∴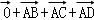
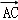
知识点
在△ABC中,边a、b、c分别是角A、B,C的对边,且满足bcosC=(3a -c)cosB。
(1)求cosB;
(2)若

正确答案
见解析。
解析
知识点
已知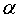
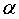
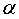
正确答案
解析
本题考查了同角三角函数的关系,二倍角公式以及两角和差的三角函数公式.由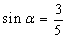
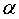
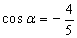
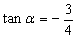
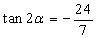
知识点
在△









正确答案
解析
略
知识点
从1,3,5,7这四个数中随机地取两个数组成一个两位数,则组成的两位数是5的倍数的概率为() 。
正确答案
解析
略
知识点








(1)求角
(2)若



正确答案
见解析。
解析
(1) 由





即
所以,
(2)由

在
得 
知识点
在△ABC中,AB=



正确答案
2
解析
略
知识点
在△ABC中,a、b、c分别为角A、B、C的对边,且满足b2 +C2 -a2= bc。
(1)求角A的值;
(2)若a=
正确答案
见解析。
解析
知识点
已知


正确答案
解析
略
知识点
在直角梯形ABCD中,AD∥BC,∠A=90°,AB=AD=1,BC=2,E是CD的中点, 则
正确答案
-1
解析
略
知识点
扫码查看完整答案与解析