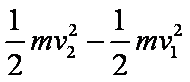- 能量守恒定律与能源
- 共104题
环保混合动力车是指使用汽油机驱动和利用蓄电池所储存的电能驱动的汽车。它可按平均需要使用的功率来确定汽油机的最大功率,此时处于油耗低、污染少的最优工况下工作。汽车需要大功率而汽油机功率不足时由电动机来补充,电动机的电源为蓄电池;汽车负荷少时,电动机可作为发电机使用,汽油机的一部分功率用来驱动汽车,另一部分功率驱动发电机,可发电给蓄电池充电。
有一质量m=1200kg的混合动力轿车,在平直公路上以v1=90km/h匀速行驶,汽油发动机的输出功率为P=60kW。当驾驶员看到前方有80km/h的限速标志时,保持汽油发动机功率不变,立即启动发电机工作给蓄电池充电,此时轿车的动力减小,做减速运动,运动距离s=80m后,速度变为v2=72km/h。此过程中汽油发动机功率的25%用于轿车的牵引,75%用于供给发电机工作,发动机输送给发电机的能量最后有50%转化为蓄电池的电能。假设轿车在上述运动过程中所受阻力保持不变。试求:
(1)轿车以90km/h在平直公路上匀速行驶时,所受阻力Ff的大小;
(2)轿车从90km/h减速到72km/h的这一过程中,蓄电池获得的电能E电;
(3)若电动机的输出功率也为60 kW,此时汽油发动机和电动机共同工作的最大功率可以达到Pm=108kW,汽车驶上与水平地面成30°角斜坡,汽车爬坡过程中所受阻力为重力的0.1倍,设斜坡足够长,求汽车在斜坡上做匀速运动的最大速度vm。(g取10m/s2)
正确答案
见解析。
解析
(1)轿车以ν1=90km/h=25m/s匀速行驶时,汽车受到的阻力等于牵引力,有
P=Ff ν1
解得阻力 Ff = 2.4×103N
(2)轿车做减速运动s=80m速度减为v2=72km/h=20m/s,设这一过程中汽油发动机做的总功为W,由动能定理有
W×25%—Ff ·s=
代入数据得:W=2.28×105J
蓄电池获得的电能 E电= W× 75%×50% =8.55×104J
(3)汽车在斜坡上做匀速运动时牵引力F=mgsin30°+0.1mg。在斜坡上匀速运动的最大速度设为vm,有
Pm=(mgsin30°+0.1mg)vm
可得最大速度vm=15m/s
知识点
十三陵抽水蓄能电站担负着北京地区调峰和紧急事故备用电源,改善首都供电质量的重要任务。抽水蓄能电站的工作原理是,在用电低谷时,电站利用电网多余电能把水抽到高处蓄水池中,到用电高峰时,再利用蓄水池中的水发电。电站利用已建十三陵水库为下游水库,在蟒山后上寺沟头修建上游水库。电站的年发电量约为10亿kW·h,年抽水用电量约为14亿kW·h。如图所示,上游水库近似视为长方体,可用于发电的库容量为V,蓄水后上游水库水深为d,蓄水后水位高出下游水面高度为H。已知下游水库的库容量远大于上游水库的库容量。
(1)求十三陵抽水蓄能电站的总效率η;
(2)求能用于发电的水的最大重力势能EP;
(3)若把抽水蓄能电站产生的电能输送到北京城区。已知输电功率为P,输电线路的总阻值为R。要使输电线路上损耗的功率小于ΔP,
a.求输电电压的最小值U;
b.在输电功率一定时,请提出两种减少输电过程中功率损耗的方法。
正确答案
见解析。
解析
(1)总效率
(2)能用于发电的水的总质量
所以,能用于发电的水的最大重力势能
(3)a,当输电电压为U时,输电电流
所以,损失功率
所以,输电电压的最小值
b.增大输电导线的横截面积;改用电阻率小的输电导线;提高输电电压。
知识点
如图所示,固定的光滑平台上固定有光滑的半圆轨道,轨道半径R=0.6m。平台上静止着两个滑块A、B,mA=0.1Kg,mB=0.2Kg,两滑块间夹有少量炸药,平台右侧有一带挡板的小车,静止在光滑的水平地面上。小车质量为M=0.3Kg,车面与平台的台面等高,车面左侧粗糙部分长度为L=0.8m,动摩擦因数为μ=0.2,右侧拴接一轻质弹簧,弹簧自然长度所在处车面光滑。点燃炸药后,A滑块到达轨道最高点时对轨道的压力大小恰好等于A滑块的重力,滑块B冲上小车。两滑块都可以看作质点,炸药的质量忽略不计,爆炸的时间极短,爆炸后两个物块的速度方向在同一水平直线上,且g=10m/s2。求:
(1)滑块在半圆轨道最低点对轨道的压力
(2)炸药爆炸后滑块B的速度大小
(3)滑块B滑上小车后的运动过程中弹簧的最大弹性势能
正确答案
见解析。
解析
(1)在最高点由牛顿第二定律:
由已知最高点压力
由机械能守恒定律:
在半圆轨道最低点由牛顿第二定律:
解得: 
由牛顿第三定律:
滑块在半圆轨道最低点对轨道的压力大小为7N,方向竖直向下 ……(1分)
(2)由动量守恒定律:

(3)由动量守恒定律:
由能量守恒定律:

知识点
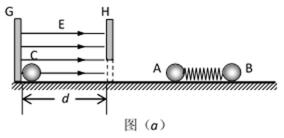
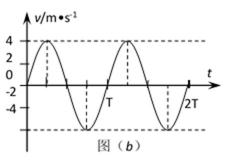
如图,光滑水平面上固定着一对竖直放置的平行金属板G和H。在金属板G右壁固定一个可视为质点的小球C,其质量为 MC=0.01kg、带电量为q=+1×10-5C。G、H两板间距离为d=10cm,板H下方开有能让小球C自由通过的小洞。质量分别为MA=0.01kg和MB=0.02kg的不带电绝缘小球A、B用一轻质弹簧连接,并用细线栓连使弹簧处于压缩状态,静放在H板右侧的光滑水平面上,如图(a)所示。现将细线烧断,小球A、B在弹簧作用下做来回往复运动(A球不会进入G、H两板间)。以向右为速度的正方向,从烧断细线断开后的某时刻开始计时,得到A球的速度—时间图象如图(b)所示。
(1)求在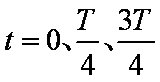
(2)若G、H板间是电场强度为E=8×104V/m的匀强电场,在某时刻将小球C释放,则小球C离开电场时的速度为多大?若小球C以离开电场时的速度向右匀速运动,它将遇到小球A,并与之结合在一起运动,试求弹簧的最大弹性势能的范围。
正确答案
见解析。
解析
(1)对于小球A、B与轻质弹簧组成的系统,当烧断细线后动量守恒,有
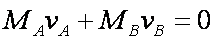
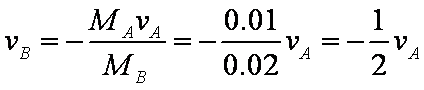
当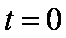
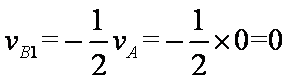
当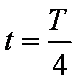
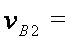
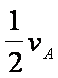
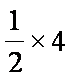
当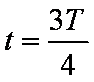
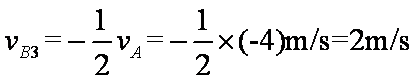
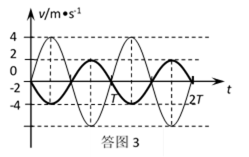
小球B的速度—时间图象如答图3所示。
(2)当金属板间加有匀强电场时,电场力对小球做功,小球获得初动能并离开金属板。
由动能定理,有
得 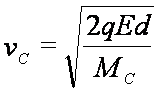
因水平方向A、B、C三小球系统不受外力,故系统动量守恒。
由此可得,不论A、C两球何时何处相碰,三球的共同速度是一个定值,即三球速度相同时的总动能是一定值。
由MCvC=(MA+MB+MC)v共 , 解得v共 =1m/s
当三球速度相同时弹簧的弹性势能最大。
当A球在运动过程中速度为4m/s且与C球同向时,跟C球相碰,系统损失能量最小(为0),此情况下三球在运动过程中弹簧具有的最大弹性势能设为E1
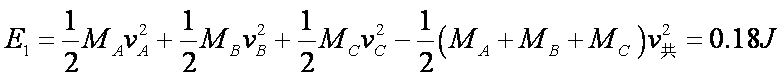
当A球在运动过程中速度为4m/s与C球反向时,跟C球相碰,系统损失能量最大,此情况下三球运动的过程中弹簧具有的最大弹性势能设为E2
由MCvC–MAvA=(MA + MC)v3 , 解得v3 =0
E2=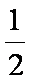
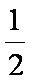
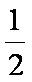
由上可得:弹簧具有的最大弹性势能的可能值在0.02J ~ 0.18J的范围内。
知识点
在交通运输中,常用“客运效率”来反映交通工具的某项效能,“客运效率”表示每消耗单位能量对应的载客数和运送路程的乘积,即客运效率=人数×路程/消耗能量。一个人骑电动自行车,消耗1MJ(106J)的能量可行驶30km,一辆载有4人的普通轿车,消耗320MJ的能量可行驶100km,则电动自行车与这辆轿车的客运效率之比是 :( )
正确答案
解析
略
知识点
扫码查看完整答案与解析