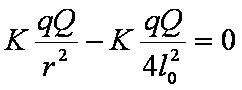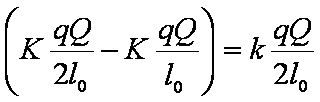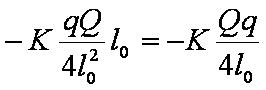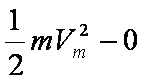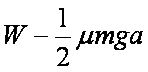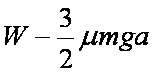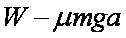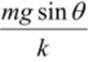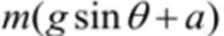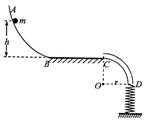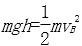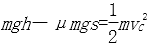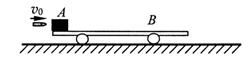- 能量守恒定律与能源
- 共104题
已知真空中电量为Q的点电荷电场中,若取无穷远为零电势点,则离电荷距离为r的某点的电势表达式为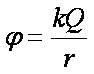
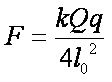
(1)乙球在释放瞬间的加速度大小;
(2)乙球的速度最大时两个电荷间的距离;
(3)乙球运动的最大速度vm为多少?
(4)乙球运动过程中,离开甲球的最大距离和最小距离是多少?
正确答案
见解析
解析
(1)乙求受到电场力和F的作用,合力
ΣF=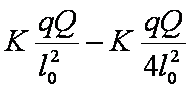
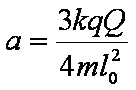
(2)合外力向左,所以乙球向左做加速度减小的加速运动,当合力为零时,速度最大
ΣF=
r =2l0
(3) 乙球的电势能: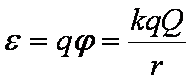
电场力做正功,等于电势能的减少:
WE=-Δε=-
外力做负功:
WF =
由动能定理:WE + WF=
得: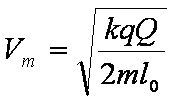
(4)乙球达到速度最大后,再向左做加速度增大的减速运动,当速度等于零时,离甲球最远。V=0此时离开甲球距离为rm ,然后又向右运动到r=l0时速度又等于零。
所以离开A球最近的距离为 l0
WE + WF=0
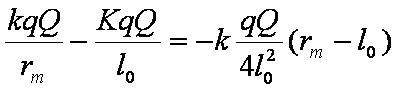
rm=4l0
所以 ( l0 ~4 l0 )
知识点
如图所示,在固定倾斜光滑杆上套有一个质量为m的圆环,杆与水平方向的夹角α=30°,圆环与竖直放置的轻质弹簧上端相连,弹簧的另一端固定在地面上的A点,弹簧处于原长h。让圆环沿杆由静止滑下,滑到杆的底端时速度恰为零。则在圆环下滑过程中
正确答案
解析
略。
知识点
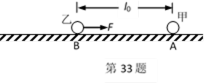
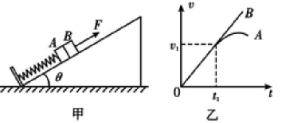
传送带被广泛应用于各行各业。由于不同的物体与传送带之间的动摩擦因数不同,物体在传送带上的运动情况也有所不同。如图所示,一倾斜放置的传送带与水平面的倾角θ=370,在电动机的带动下以v=2m/s的速率顺时针方向匀速运行。M、N为传送带的两个端点,MN两点间的距离L=7m。N端有一离传送带很近的挡板P可将传送带上的物块挡住。在传送带上的O处先后由静止释放金属块A和木块B,金属块与木块质量均为1kg,且均可视为质点,OM间距离L=3m。sin37° = 0.6,cos37°=0.8,g取10m/s2。传送带与轮子间无相对滑动,不计轮轴处的摩擦。
(1)金属块A由静止释放后沿传送带向上运动,经过2s到达M端,求金属块与传送带间的动摩擦因数μ1。
(2)木块B由静止释放后沿传送带向下运动,并与挡板P发生碰撞。已知碰撞时间极短,木块B与挡板P碰撞前后速度大小不变,木块B与传送带间的动摩擦因数μ2=0.5。求:
a.与挡板P第一次碰撞后,木块B所达到的最高位置与挡板P的距离;
b.经过足够长时间,电动机的输出功率恒定,求此时电动机的输出功率。
正确答案
见解析。
解析
(1)金属块A在传送带方向上受摩擦力和重力的下滑分力,先做匀加速运动,并设其速度能达到传送带的速度v=2m/s,然后做匀速运动,达到M点。
金属块由O运动到M有 

且 t1+t2=t 即 t1+t2=2 ②
v=at1 即 2=at1 ③………1分
根据牛顿第二定律有 
由①②③式解得 t1=1s<t=2s 符合题设要求,加速度a=2m/s2
由①式解得金属块与传送带间的动摩擦因数μ1=1
(2)a. 由静止释放后,木块B沿传送带向下做匀加速运动,其加速度为a1,运动距离LON=4m,第一次与P碰撞前的速度为v1


与挡板P第一次碰撞后,木块B以速度v1被反弹,先沿传送带向上以加速度a2做匀减速运动直到速度为v,此过程运动距离为s1;之后以加速度a1继续做匀减速运动直到速度为0,此时上升到最高点,此过程运动距离为s2。



因此与挡板P第一次碰撞后,木块B所达到的最高位置与挡板P的距离
b. 木块B上升到最高点后,沿传送带以加速度a1向下做匀加速运动,与挡板P发生第二次碰撞,碰撞前的速度为v2

与挡板第二次碰撞后,木块B以速度v2被反弹,先沿传送带向上以加速度a2做匀减速运动直到速度为v,此过程运动距离为s3;之后以加速度a1继续做匀减速运动直到速度为0,此时上升到最高点,此过程运动距离为s4。


木块B上升到最高点后,沿传送带以加速度a1向下做匀加速运动,与挡板P发生第三次碰撞,碰撞前的速度为v3

与挡板第三次碰撞后,木块B以速度v3被反弹,先沿传送带向上以加速度a2做匀减速运动直到速度为v,此过程运动距离为s5;之后以加速度a1继续做匀减速运动直到速度为0,此时上升到最高点,此过程运动距离为s6。


以此类推,经过多次碰撞后木块B以2m/s的速度被反弹,在距N点1m的范围内不断以加速度a2做向上的减速运动和向下的加速运动。
木块B对传送带有一与传送带运动方向相反的阻力

故电动机的输出功率
解得P=8w
知识点
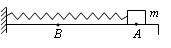
如图所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连。弹簧处于自然长度时物块位于O点(图中未标出)。物块的质量为m,物块与桌面间的动摩擦因数为μ。现用水平向右的力将物块从O点缓慢拉至A点,拉力做的功为W。撤去拉力后物块由静止向左运动,经O点到达B点时速度减小为零,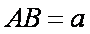
正确答案
解析
略。
知识点
有一质量m=1000kg的轿车,在平直公路上以ν1=90km/h的速度匀速行驶,此时发动机的输出功率P=50kW,全部用于轿车的牵引。某时刻起,保持发动机的输出功率不变,启动利用电磁阻尼带动的电动机为车载蓄电池充电,轿车做减速运动。运动L=72m后,轿车速度变为ν2=72km/h,此过程中发动机输出功率的20%用于轿车的牵引,80%用于供给发电机工作,发电机获得能量的50%转化为蓄电池的电能。假设轿车在上述运动过程中所受阻力保持不变。
(1)求轿车运动中受到的阻力F阻的大小;
(2)求在上述过程中蓄电池获得的电能E电的大小;
(3)若该车可以利用所储存的电能作为动力来源,则轿车仅用上述过程中获得的电能E电维持匀速运动,能行驶的距离L’的大小是多少?
正确答案
见解析。
解析
(1)ν1=90km/h=25m/s,ν2=72km/h=20m/s
匀速行驶时P=F阻ν1,
(2)设这一过程中汽车发动机做的总功为W,根据动能定理有:
20%W-W阻=
E电=50%×80%W=6.3×104J
(3)汽车维持匀速运动,电能全部用于克服阻力做功
E电=F阻L’,代入数据可得L’=31.5m
知识点
如图所示,质量分别为m1和m2的两个小球A、B,带有等量异种电荷,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上。当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是
正确答案
解析
略
知识点
随着能源危机的不断加剧,我们不但要合理节约常规能源,还要大力开发新能源,下列能源中属于新能源的是
正确答案
解析
略
知识点
如图所示,平行于光滑固定斜面的轻弹簧劲度系数为k,一端固定在倾角为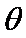
正确答案
解析
略。
知识点
如图所示,光滑曲面AB与水平面BC平滑连接于B点,BC右端连接内壁光滑、半径为r=0.4m的四分之一细圆管CD,管口D端正下方直立一根劲度系数为k=25N/m的轻弹簧,轻弹簧下端固定,上端恰好与管口D端齐平。质量为m=l kg的小球在曲面上距BC的高度为h=0.8m处从静止开始下滑,进入管口C端时与管壁间恰好无作用力,通过CD后压缩弹簧。已知弹簧的弹性势能表达式为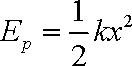
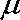
(1)小球达到B点时的速度大小vB;
(2)水平面BC的长度s;
(3)在压缩弹簧过程中小球的最大速度vm。
正确答案
(1)vB=4m/s
(2)s=1.2m
(3)vm=4m/s
解析
(1)由机械能守恒得:
解得:vB=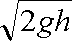
(2)由mg=m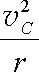
得vC=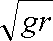
由动能定理得:
解得:s=1.2m
(3)设在压缩弹簧过程中小球速度最大时离D端的距离为x,则有:
kx=mg
得:x=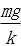
由功能关系得: mg(r+x)-


解得: vm=4m/s
知识点
(1)氘核





(2)质量为mB=2kg的平板车B上表面水平,开始时静止在光滑水平面上,在平板车左端静止着一块质量为mA=2kg的物块A,一颗质量为m0=0.01kg的子弹以v0=600m/s的水平初速度瞬间射穿A后,速度变为v=100m/s,已知A、B之间有摩擦,且平板车B足够长。求:
①物块A的最大速度vA;
②平板车B的最大速度vB
正确答案
(1)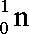
(2)①vA=2.5m/s;②vB=1.25m/s
解析
(1)略。
(2)①子弹穿过物体A的过程中,对子弹和物块A,由动量守恒定律得:
m0v0=m0v+mAvA
解得:vA=2.5m/s
②对物块A和平板车B,由动量守恒定律得:
mAvA=(mA+mB)vB
解得:vB=1.25m/s
知识点
扫码查看完整答案与解析