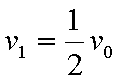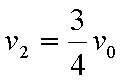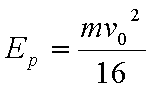- 能量守恒定律与能源
- 共104题
节能混合动力车是一种可以利用汽油及所储存电能作为动力来源的汽车。有一质量m=1000kg的混合动力轿车,在平直公路上以v1=90km/h匀速行驶,发动机的输出功率为P=50kW。当驾驶员看到前方有80km/h的限速标志时,保持发动机功率不变,立即启动利用电磁阻尼带动的发电机工作给电池充电,使轿车做减速运动,运动L=72m后,速度变为v2=72km/h。此过程中发动机功率的1/5用于轿车的牵引,4/5用于供给发电机工作,发动机输送给发电机的能量最后有50%转化为电池的电能。假设轿车在上述运动过程中所受阻力保持不变。求
(1)轿车以90km/h在平直公路上匀速行驶时,所受阻力F阻的大小;
(2)轿车从90km/h减速到72km/h过程中,获得的电能E电;
(3)轿车仅用其在上述减速过程中获得的电能E电维持72km/h匀速运动的距离L′。
正确答案
见解析。
解析
(1)汽车牵引力与输出功率的关系
将
当轿车匀速行驶时,牵引力与阻力大小相等,有
(2)在减速过程中,注意到发动机只有

电源获得的电能为
(3)根据题设,轿车在平直公路上匀速行驶时受到的阻力仍为

代入数据得
知识点
(1)关于原子核的结合能,下列说法正确的是
a.原子核的结合能等于使其完全分解成自由核子所需的最小能量
b.一重原子核衰变成α粒子和另一原子核,衰变产物的结合能之和一定大于原来重核的结合能
c. 铯原子核(

d.比结合能越大,原子核越不稳定
e.自由核子组成原子核时,其质量亏损所对应的能量大于该原子核的结合能
(2)如图,光滑水平直轨道上有三个质量均为m的物块A、B、C。 B的左侧固定一轻弹簧(弹簧左侧的挡板质最不计)。设A以速度V0朝B运动,压缩弹簧;当A、 B速度相等时,B与C恰好相碰并粘接在一起,然后继续运动。假设B和C碰撞过程时间极短。求从A开始压缩弹簧直至与弹簧分离的过程中,
① 整个系统损失的机械能;
② 弹簧被压缩到最短时的弹性势能。
正确答案
答案:(1)ABC
(2)
(3)
解析
略
知识点
(1)氢原子能级如图,当氢原子从

a. 氢原子从

b. 用波长为325nm的光照射,可使氢原子从

c. 一群处于
d. 用波长为633nm的光照射,不能使氢原子从

(2)如图,光滑水平直轨道上两滑块A.B用橡皮筋连接,A的质量为m。开始时橡皮筋松驰,B静止,给A向左的初速度v0。一段时间后,B与A同向运动发生碰撞并粘在一起。碰撞后的共同速度是碰撞前瞬间A的速度的两倍,也是碰撞前瞬间B的速度的一半。求:
(ⅰ)B的质量;
(ⅱ)碰撞过程中A.B系统机械能的损失。
正确答案
(1)cd
(2)解:
(ⅰ)以初速度v0的方向为正方向,设B的质量为mB,A.B碰撞后的共同速度为v,由题意知:碰撞前瞬间A的速度为

由①式得 
(ⅱ)从开始到碰后的全过程,由动量守恒定律得

设碰撞过程A.B系统机械能的损失为

联立②③④式,得
解析
略。
知识点
如图所示,质量为






(1)求物块处于平衡位置时弹簧的长度;
(2)选物块的平衡位置为坐标原点,沿斜面向下为正方向建立坐标轴,用
(3)求弹簧的最大伸长量;
(4)为使斜面始终处于静止状态,动摩擦因数
正确答案
见解析
解析
(1)设物块在斜面上平衡时,弹簧伸长量为x,有


(2)由物块所受
得 :
解得:
符合简谐振动的回复力特征,所以是简谐振动.
(3)物块做简谐振动的振幅为

(4)物块运动时,要斜面静止则需要
在物块具有最大向上加速度时保持不动,则整个过程保持不动
联立求解得:
知识点
图18,两块相同平板P1、P2至于光滑水平面上,质量均为m。P2的右端固定一轻质弹簧,左端A与弹簧的自由端B相距L。物体P置于P1的最右端,质量为2m且可以看作质点。P1与P以共同速度v0向右运动,与静止的P2发生碰撞,碰撞时间极短,碰撞后P1与P2粘连在一起,P压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内)。
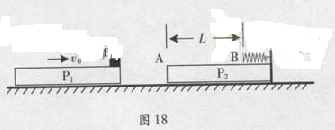
(1)P1、P2刚碰完时的共同速度v1和P的最终速度v2;
(2)此过程中弹簧最大压缩量x和相应的弹性势能Ep
正确答案
见解析
解析
(1)p1和p2碰撞动量守恒:
mv0=(m+m)v1 ①
得出:
P在p2上滑行过程 p1、p2、p系统动量守恒:
2mv0+2mv1=4mv2 ②
得出:
(2)p1 p2 p第一次等速弹簧最大压缩量最大,由能量守恒得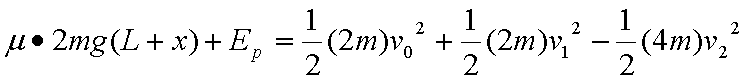
p刚进入p2 到p1 p2 p 第二次等速时有能量守恒得;
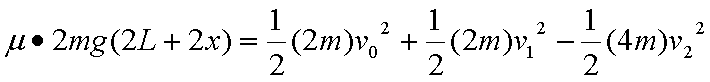
由③④得: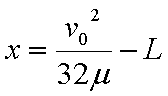
知识点
扫码查看完整答案与解析