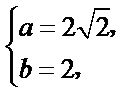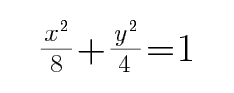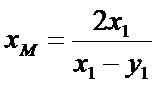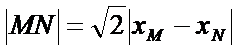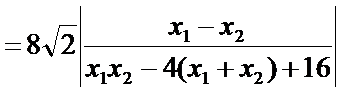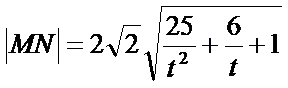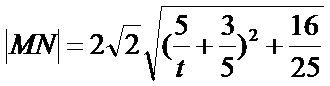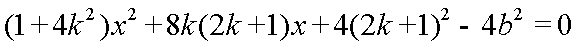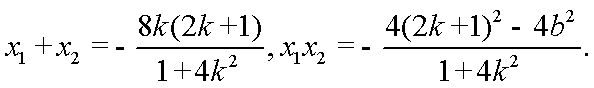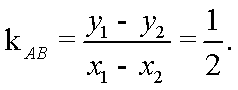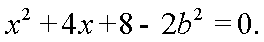- 直线、圆及圆锥曲线的交汇问题
- 共263题
8.双曲线

正确答案
解析
双曲线

双曲线

可得:


即




故选A.
考查方向
解题思路
先根据双曲线方程求得双曲线的渐近线,进而利用圆心到渐近线的距离为圆的半径求得a和b的关系,进而利用
易错点
直线与圆相切,圆心到直线的距离等于半径.
知识点
发达国家应该______自己的历史责任和当前人均排放高的现实,严格______《京都议定书》确定的减排目标,继续承担中期大幅量化减排义务。 填入横线部分最恰当的一项是( )。
A.承担 遵守
B.正视 履行
C.重视 遵守
D.直面 履行
正确答案
B
解析
[解析] “承担”与“现实”不能搭配。“正视”,用严肃认真的态度对待,不躲避,不敷衍。“直面”,当面,面对。对于自己的历史责任和当前人均排放高的现实,发达国家应该用严肃认真的态度来对待,B项正确。
在平面直角坐标系
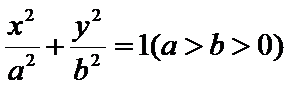
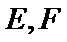
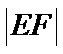
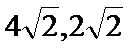
23.求椭圆的方程;
24.与圆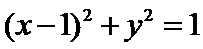
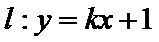
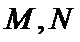
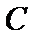
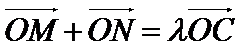
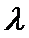
正确答案
(Ⅰ)由题意知,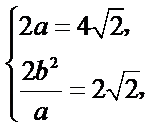
所求椭圆的方程为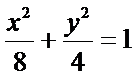

解析
由题意,得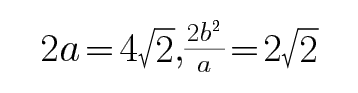
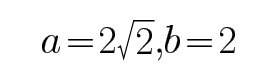
考查方向
本题考查椭圆焦点弦知识,由焦点弦的公式可以知道最大值与最小值
解题思路
由焦点弦公式,可得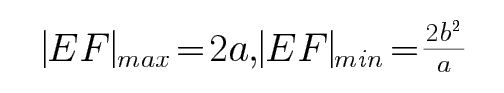
易错点
焦点弦的最大值与最小值容易弄错
教师点评
本题只需要记住焦点弦的公式就可以解决,在近几年中考到的频率较高,是解析几何中重要的一块
正确答案
(Ⅱ)设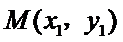
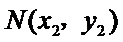
由直线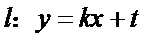
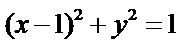
所以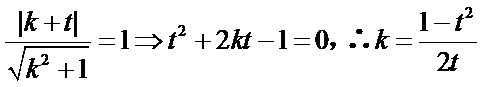
联立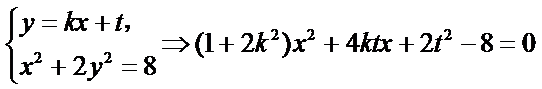
所以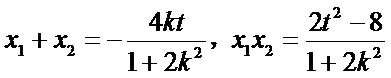
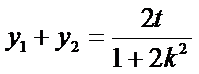
又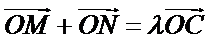
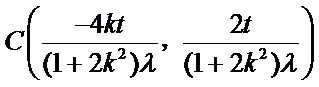
将点C代入椭圆方程并化简得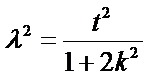
①代入②得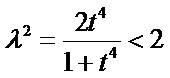
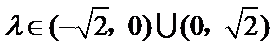
解析
(Ⅱ)设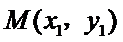
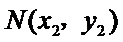
由直线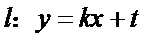
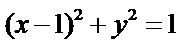
所以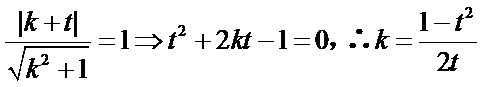
联立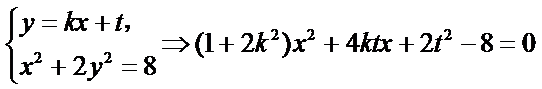
所以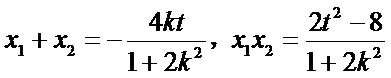
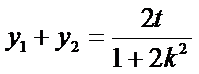
又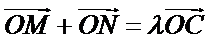
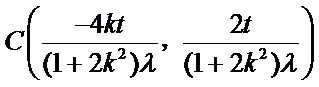
将点C代入椭圆方程并化简得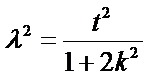
①代入②得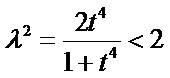
考查方向
本题考查圆与直线相切问题,向量在圆锥曲线上的应用,变量取值范围问题
解题思路
先由圆与直线相切,求出k,然后联立直线与椭圆方程,消去一个元,算出两根和积,再结合向量的性质,联立关系式,求出变量取值范围
易错点
容易算错斜率,以及变量的取值范围
教师点评
本题是圆锥曲线中的常规题,难度是中等,需要掌握切线问题、设而不求法、向量等知识,才能求出变量的取值范围,在近几年中考到的频率较高,是解析几何中重要的一块
已知抛物线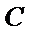
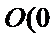
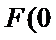
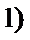
23.求抛物
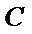
24.过点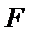
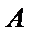
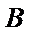
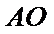
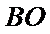
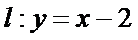
正确答案
解:由题意,设抛物线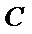
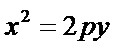
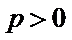
则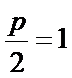
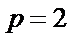
所以抛物线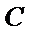
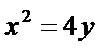
解析
解:由题意,设抛物线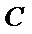
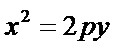
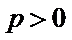
则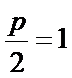
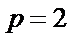
所以抛物线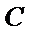
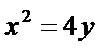
考查方向
抛物线的标准方程
解题思路
熟练掌握抛物线的四种形式即可求解。
易错点
容易把抛物线的对称轴弄反了。
教师点评
熟记抛物线的标准方程是关键。
正确答案
解:由题意,直线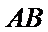
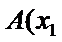
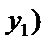
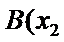
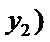
直线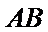
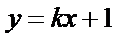
由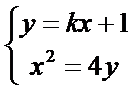
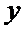
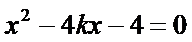
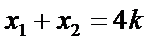
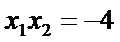
从而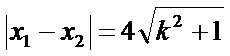

由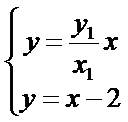
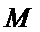
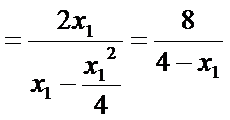
同理点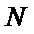
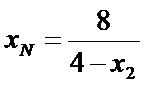
所以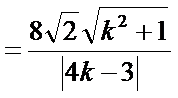
令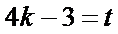
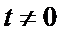
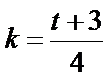
当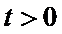
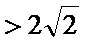
当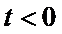
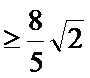
综上所述,当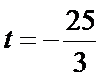
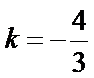
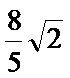
解析
解:由题意,直线
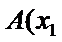
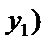
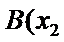
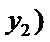
直线
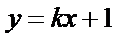
由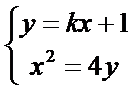
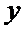
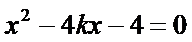
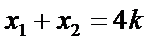
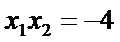
从而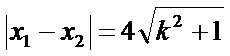

由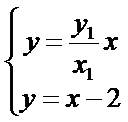
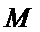
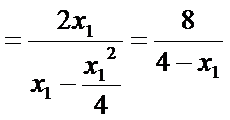
同理点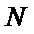
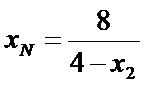
所以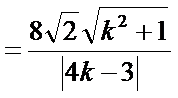
令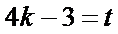
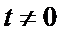
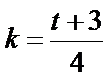
当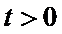
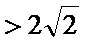
当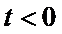
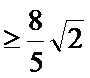
综上所述,当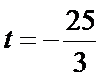
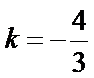
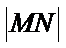
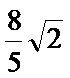
考查方向
弦长公式及最值问题。
解题思路
联立直线和抛物线的方程,然后用韦达定理的两根的关系,再同弦长公式表示出来,最后配方得到最小值。
易错点
1、解方程出错;2、将弦长公式表示出来后,没有思路。
教师点评
本题考查了抛物线的标准方程及直线与抛物线的位置关系,弦长公式、最值问题。
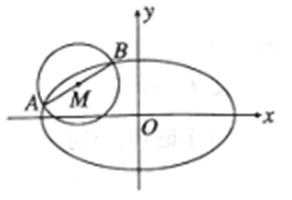
20.已知椭圆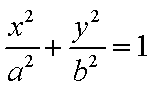
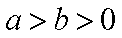


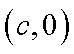
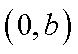
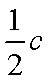
(1)求椭圆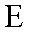
(2)如图,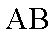
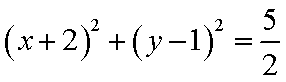
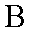
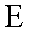
正确答案
(1)过点(c,0),(0,b)的直线方程为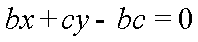
则原点O到直线的距离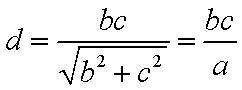
由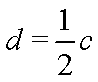
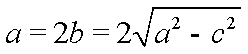
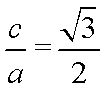
(2)解法一:由(1)知,椭圆E的方程为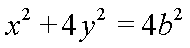
依题意,圆心M(-2,1)是线段AB的中点,且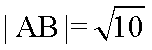
易知,AB不与x轴垂直,设其直线方程为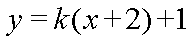
设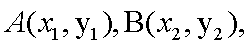
由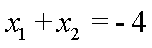
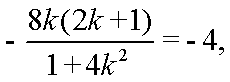
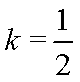
从而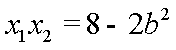
于是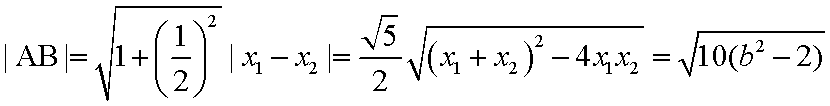
由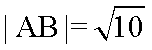
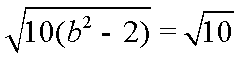
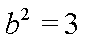
故椭圆E的方程为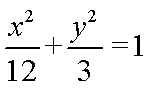
解法二:由(I)知,椭圆E的方程为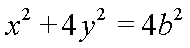
依题意,点A,B关于圆心M(-2,1)对称,且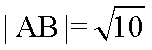
设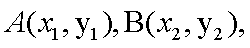
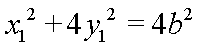
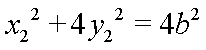
两式相减并结合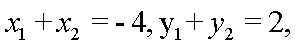
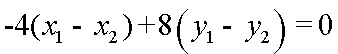
易知,AB不与x轴垂直,则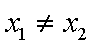
因此AB直线方程为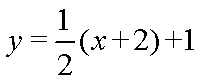
所以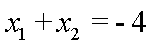
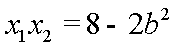
于是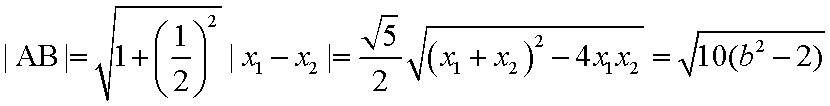
由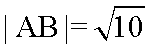
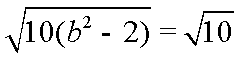
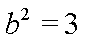
故椭圆E的方程为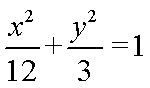
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析