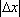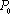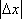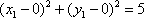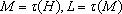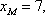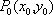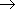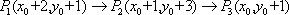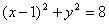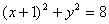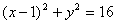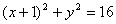- 圆的方程
- 共277题
已知圆C:

正确答案
解析
略
知识点
已知平面上点




正确答案
解析
略
知识点
已知椭圆

(1)求椭圆
(2)直线







正确答案
见解析。
解析
(1)∵椭圆


又∵椭圆经过点

∴故所求椭圆方程为
(2)设



当直线



所以

所以



当直线


所以

当

方程有两个不同的解又

所以


代入

又原点到直线的距离为
所以
考虑到







综上,

知识点
若圆C经过(1,0),(3,0)两点,且与y轴相切,则圆C的
方程为
正确答案
解析
略
知识点
已知圆心在第一象限的圆C经过坐标原点O,与x轴的正半轴交于另一个点A,且∠OCA=120°,该圆截x轴所得弦长为2,则圆C的标准方程为 ▲ 。
正确答案
解析
略
知识点
设函数f(x)=x3+2ax2+bx+a,g(x)=x2-3x+2,其中x∈R,a、b为常数,已知曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线l.
(1)求a、b的值,并写出切线l的方程;
(2)若方程f(x)+g(x)=mx有三个互不相同的实根0、x1、x2,其中x1<x2,且对任意的x∈[x1,x2],f(x)+g(x)<m(x-1)恒成立,求实数m的取值范围。
正确答案
见解析。
解析
(1)

由于曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线,
故有f(2)=g(2)=0,

由此得
所以a=-2,b=5,切线l的方程为x-y-2=0.
(2)由(1)得f(x)=x3-4x2+5x-2,
所以f(x)+g(x)=x3-3x2+2x.
依题意,方程x(x2-3x+2-m)=0有三个互不相同的实根0、x1、x2,
故x1、x2是方程x2-3x+2-m=0的两相异的实根。
所以Δ=9-4(2-m)>0,即m>-
又对任意的x∈[x1,x2],f(x)+g(x)<m(x-1)恒成立。
特别地,取x=x1时,f(x1)+g(x1)-mx1<-m成立,得m<0.
由韦达定理,可得x1+x2=3>0,x1x2=2-m>0,
故0<x1<x2.
对任意的x∈[x1,x2],有x-x2≤0,x-x1≥0,x>0,
则f(x)+g(x)-mx=x(x-x1)(x-x2)≤0,
又f(x1)+g(x1)-mx1=0,
所以函数f(x)+g(x)-mx在x∈[x1,x2]的最大值为0.
于是当-
综上,m的取值范围是
知识点
设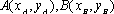
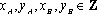
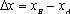
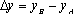
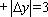
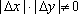
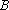
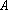
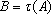
(1)请问:点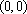
(2)已知点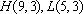
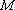
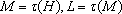
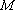
(3)已知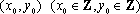
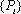
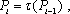
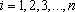
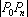
正确答案
见解析
解析
(1)因为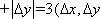
故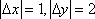
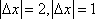
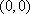

所以这些可能值对应的点在以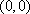

(2)设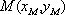
所以有
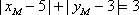
所以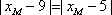
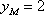
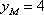
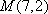
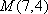
(3)当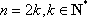
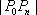
当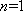
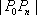

当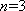

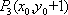
故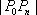
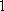
当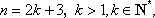

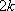
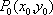
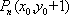
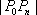
综上,当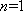
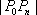
当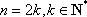
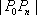
当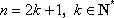
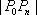
知识点
已知曲线





正确答案
解析
略
知识点
已知圆










(1)求直线
(2)求圆
正确答案
见解析。
解析
(1)(法一)∵点

∴直线


(法二)当直线

当直线




则圆心




∴直线

(2)设圆



∴圆

∵圆






整理得:


∵

∴圆

知识点
以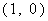
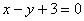
正确答案
解析
略
知识点
扫码查看完整答案与解析