- 直线与圆、圆与圆的位置关系
- 共336题
在平面直角坐标系
上至少存在一点，使得以该点为圆心，1为半径的圆与圆
正确答案
解析
∵圆C的方程可化为：
∵由题意，直线
∴存在
∵
∴
知识点
过点（-1,2）的直线l被圆
正确答案
1或
解析
由题意，直线与圆要相交，斜率必须存在，设为
知识点
直线
A1
B2
C4
D
正确答案
解析
圆心
知识点
已知圆C过点（1,0），且圆心在x轴的正半轴上，直线l：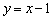
的弦长为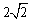
正确答案
解析
由题意，设圆心坐标为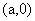
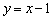
的弦长为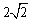
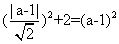
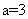
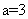
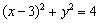
知识点
将圆x2＋y2－2x－4y＋1＝0平分的直线是( )
正确答案
解析
圆x2＋y2－2x－4y＋1＝0可化为标准方程
(x－1)2＋(y－2)2＝4，要使直线平分此圆，则直线需过圆心(1,2)，代入检验，C项满足条件，故选C
知识点
过直线x＋y－
正确答案
解析
如图所示，过点P作圆x2+y2=1的两条切线，切点分别为A，B，
由已知得，∠APO=30°，
所以|PO|=2.
设P点坐标为(x0，y0)，
则
故所求点P坐标为
知识点
已知圆
A
B
C
D以上三个选项均有可能
正确答案
解析
因为点P（3,0）在圆的内部，所以过点P的直线必与圆相交.选A.
知识点
过点P(1,1)的直线将圆形区域{(x，y)|x2＋y2≤4}分为两部分，使得这两部分的面积之差最大，则该直线的方程为( )
正确答案
解析
当OP与该直线垂直时，符合题意；此时kOP＝1，故所求直线斜率k＝－1.又已知直线过点P(1,1)，因此，直线方程为y－1＝－(x－1)，即x＋y－2＝0.
知识点
，在极坐标中，已知圆
正确答案
解析
∵圆
∴在
∴圆
∵圆
∴圆
知识点
已知点M(a,b)在圆
正确答案
解析
点M(a, b)在圆
知识点
扫码查看完整答案与解析