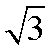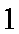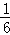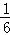- 圆的方程
- 共277题
下列使用类比推理所得结论正确的序号是 。
(1)直线a,b,c,若a∥b,b∥c,则a∥c,类推出:向量


(2)同一平面内,三条不同的直线a,b,c,若a⊥c,b⊥c,则a∥b,类推出:空间中,三条不同的直线a,b,c,若a⊥c,b⊥c,则a∥b。
(3)任意a,b∈R,a﹣b>0则a>b,类比出:任意a,b∈C,a﹣b>0则a>b。
(4)以点(0,0)为圆心,r为半径的圆的方程是x2+y2=r2,类推出:以点(0,0,0)为球心,r为半径的球的方程是x2+y2+z2=r2。
正确答案
(4)
解析
本题考查的知识点是类比推理,我们根据判断命题真假的办法,对四个答案中类比所得的结论逐一进行判断,即可得到答案。
解:(1)若向量



(2)空间内,直线a与b可以相交、平行、异面,故(2)不正确;
(3)若a,b∈C,当a=1+i,b=i时,a﹣b=1>0,但a,b 是两个虚数,不能比较大小,故(3)不正确;
(4)设点P(x,y,z)是球面上的任一点,由|OP|=r,得
故答案为:(4)。
知识点
若直线



正确答案
解析
略
知识点
在ΔABC中,三个内角






(1)求证:ΔABC
(2)设圆O过A,B,C三点,点P位于劣弧上,



正确答案
见解析
解析
(1)证明:由正弦定理得

即sin2A=sin2B ∴2A=2B或2A+2B=π,即A=B或A+B=
∵
由A+B=可知c=,∴ΔABC是直角三角形
(2)由(1)及

在RtΔ


因为
当



知识点
如图所示,已知椭圆








(1)写出抛物线
(2)求证:以AB为直径的圆过原点;
(3)若坐标原点关于直线





正确答案
见解析
解析
(1)设抛物线的标准方程为



(2)可设


设

即以
(3)设



又由

知识点
若圆心在





正确答案
解析
设圆心为



知识点
在平面直角坐标系








(1)若

(2)过









正确答案
见解析。
解析
(1)解法一:因为x1=


解法二:


因为
又x22+y22=1,联立消去y2得50 x22-30
解得

解法三:因为x



所以
由


(2)
因为

所以
因为
所以


知识点
如图,已知F1、F2分别为椭圆


(1)求椭圆C1的方程;
(2)已知点P(1,3)和圆O:x2+y2=b2,过点P的动直线l与圆O相交于不同的两点A,B,在线段AB上取一点Q,满足:

求证:点Q总在某条定直线上。
正确答案
见解析。
解析
(1)解法一:利用抛物线的方程和定义即可求出点M的坐标,再利用椭圆的定义即可求出;
解法二:同解法一求出点M的坐标,再利用椭圆的标准方程及参数a,b,c的关系即可求出。
(2)方法一:利用已知向量相等及点A,B在圆上满足圆的方程即可证明;
方法二:利用向量相等、直线与圆相交问题得到根与系数的关系即可证明。
解:(1)解法一:令M为(x0,y0),因为M在抛物线C2上,故
又

由①②解得
椭圆C1的两个焦点为F1(0,1),F2(0,﹣1),点M在椭圆上,由椭圆定义,得2a=|MF1|+|MF2|=
∴a=2,又c=1,∴b2=a2﹣c2=3
∴椭圆C1的方程为
解法二:同上求得M,而点M在椭圆上,故有

又c=1,即b2=a2﹣1,解得a2=4,b2=3∴椭圆C1的方程为
(2)证明:方法一:设A(x1,y1),B(x2,y2),Q(x,y)
由
即
由
⑤×⑦得
两式相加,得
又点A,B在圆x2+y2=3上,∴
即x+3y=3,故点Q总在直线x+3y=3上
方法二:
由

由

∴

当斜率不存在时,由特殊情况得到
当斜率存在时,设直线为y=k(x﹣1)+3
∴
代入(*)得
而
知识点
过点

正确答案
解析
知识点
直线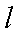
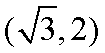
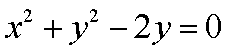
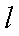
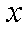
正确答案
解析
直线方程为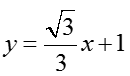
知识点
若正方体ABCD﹣A1B1C1D1的棱长为1,则三棱锥A﹣BDA1的体积为 。
正确答案
解析
三棱锥A﹣BDA1的体积就等于三棱锥A1﹣BDA的体积,
根据体积公式,
∵s=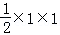

∴
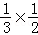
知识点
扫码查看完整答案与解析