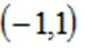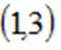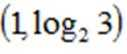- 其它不等式的解法
- 共44题
若集合
A
B
C
D
正确答案
解析
由
知识点
已知
（1）求实常数
（2）
正确答案
见解析。
解析
（1）
（2）
不等式即
即
知识点
已知
（1）指出
（2）
正确答案
见解析。
解析
（1）
（2）因为
不等式即为
∵
①若
②若
③若
知识点
已知f(x)＝|ax＋1|(a∈R)，不等式f(x)≤3的解集为{x|－2≤x≤1}。
(1)求a的值；
(2)若
正确答案
(1)2； (2) k≥1
解析
(1)由|ax＋1|≤3得－4≤ax≤2。
又f(x)≤3的解集为{x|－2≤x≤1}，所以当a≤0时，不合题意。
当a＞0时，
(2)记h(x)＝f(x)－
则
所以|h(x)|≤1，因此k≥1
知识点
已知函数f(x)＝
正确答案
解析
可画出|f(x)|的图象如图所示。
当a＞0时，y＝ax与y＝|f(x)|恒有公共点，所以排除B，C；
当a≤0时，若x＞0，则|f(x)|≥ax恒成立。
若x≤0，则以y＝ax与y＝|－x2＋2x|相切为界限，
由
∵Δ＝(a＋2)2＝0，∴a＝－2.
∴a∈[－2,0]，故选D.
知识点
已知函数
正确答案
解析
略
知识点
若
正确答案
1
解析
略
知识点
16．函数
A
B
C
D
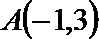
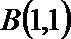
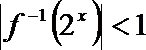
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7.函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．设函数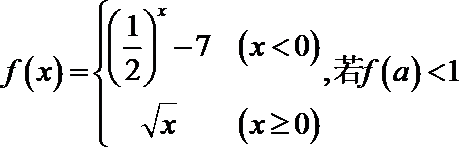
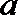
正确答案
（-3，1）
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析