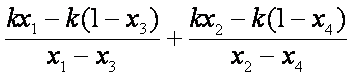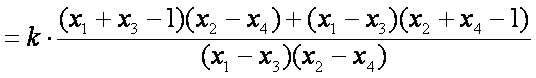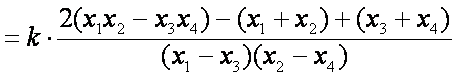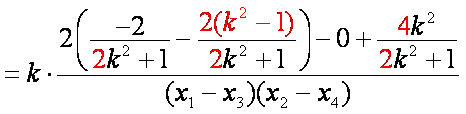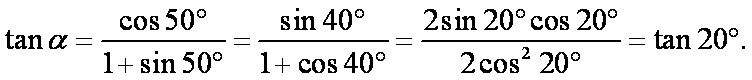- 圆系方程
- 共49题
1
题型:简答题
|
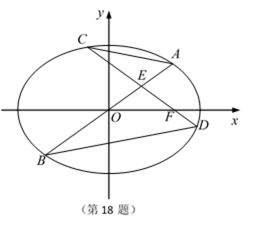
如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点

(1)求sin2θ的值;
(2) 若
正确答案
见解析
解析
(1) 因点C在


所以由三角函数定义知cosθ=
所以sin2θ=2sinθcosθ=
(2) 因为

所以
又∠

而

故点A的横坐标
知识点
圆系方程
1
题型:简答题
|
设





(1)求数列
(2)若

正确答案
见解析。
解析
(1)由已知得:

设数列



又



由题意得
故数列

(2)由(1)得



知识点
圆系方程
1
题型:简答题
|
如图,在平面直角坐标系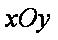
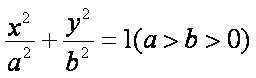
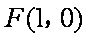
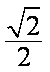
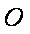
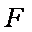
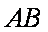
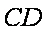
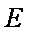
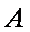
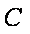
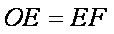
(1)求椭圆的方程;
(2)求证:直线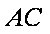
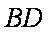
正确答案
见解析。
解析
(1)由题意,得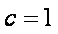
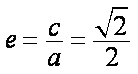
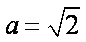
从而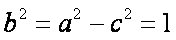
所以椭圆的方程为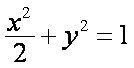
(2)证明:设直线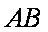
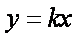
直线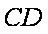
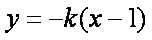
由①②得,点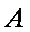
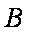
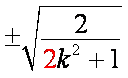
由①③得,点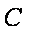
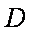
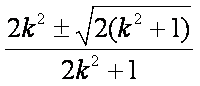
记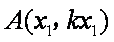
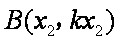
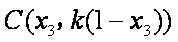
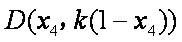
则直线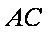
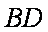
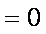
知识点
圆系方程
1
题型:
单选题
|
已知锐角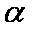
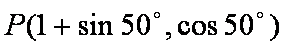
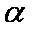
正确答案
C
解析
又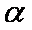
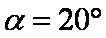
知识点
圆系方程
1
题型:简答题
|
如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若
(1)求∠AEC的大小;
(2)求AE的长。
正确答案
(1)60°(2)
解析
解析:
知识点
圆系方程
下一知识点 : 相交弦所在直线的方程
扫码查看完整答案与解析