- 相交弦所在直线的方程
- 共19题
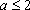
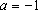
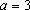
正确答案
π
解析
T=||=||=π。
知识点
从一堆苹果中任取10只,称得它们的质量如下(单位:克)
125 120 122 105 130 114 116 95 120 134
则样本数据落在
正确答案
解析
在

知识点
已知函数


正确答案
解析
∵
∴lg(log210)=lg(lg 2)-1=-lg(lg 2)。
令g(x)=ax3+bsin x,易知g(x)为奇函数。
∵f(lg(log210))=f(-lg(lg 2))=g(-lg(lg 2))+4=5,∴g(-lg(lg 2))=1.∴g(lg(lg 2))=-1.
∴f(lg(lg 2))=g(lg(lg 2))+4=-1+4=3.
知识点
方程


正确答案
解析
因为







知识点
若直线l与曲线C满足下列两个条件:
(i)直线l在点P(x0,y0)处与曲线C相切;(ii)曲线C在点P附近位于直线l的两侧,则称直线l在点P处“切过”曲线C。
下列命题正确的是 _________ (写出所有正确命题的编号)。
①直线l:y=0在点P(0,0)处“切过”曲线C:y=x3
②直线l:x=﹣1在点P(﹣1,0)处“切过”曲线C:y=(x+1)2
③直线l:y=x在点P(0,0)处“切过”曲线C:y=sinx
④直线l:y=x在点P(0,0)处“切过”曲线C:y=tanx
⑤直线l:y=x﹣1在点P(1,0)处“切过”曲线C:y=lnx。
正确答案
①③④
解析
对于①,由y=x3,得y′=3x2,则y′|x=0=0,直线y=0是过点P(0,0)的曲线C的切线,
又当x>0时y>0,当x<0时y<0,满足曲线C在P(0,0)附近位于直线y=0两侧,
∴命题①正确;
对于②,由y=(x+1)2,得y′=2(x+1),则y′|x=﹣1=0,
而直线l:x=﹣1的斜率不存在,在点P(﹣1,0)处不与曲线C相切,
∴命题②错误;
对于③,由y=sinx,得y′=cosx,则y′|x=0=1,直线y=x是过点P(0,0)的曲线的切线,
又x∈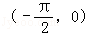
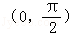
∴命题③正确;
对于④,由y=tanx,得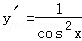
又x∈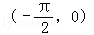
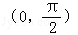
∴命题④正确;
对于⑤,由y=lnx,得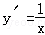
由g(x)=x﹣1﹣lnx,得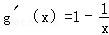
当x∈(1,+∞)时,g′(x)>0。
∴g(x)在(0,+∞)上有极小值也是最小值,为g(1)=0。
∴y=x﹣1恒在y=lnx的上方,不满足曲线C在点P附近位于直线l的两侧,
命题⑤错误。
∴正确的命题是①③④。
知识点
扫码查看完整答案与解析