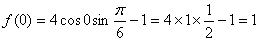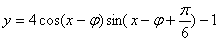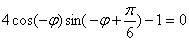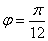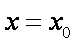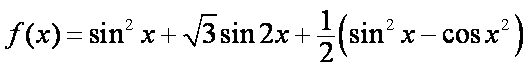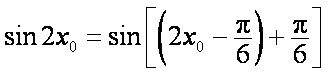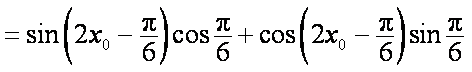- 余弦函数的图象
- 共14题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数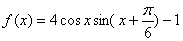
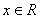
(1)求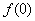
(2)若将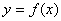
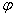
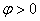
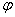
正确答案
见解析。
解析
(1)
(2)向右平移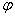
曲线经过坐标原点,得
化简(和差化积或积化和差),得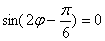
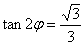
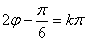
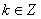
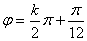
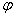
知识点
在


(1)若





(2)若


正确答案
见解析。
解析
(1)∵

∴
由余弦定理及已知条件得,
又因为



联立方程组
解得

(2) ∵
∴

∴

知识点
甲、乙、丙三人参加一项技能测试,已知甲通过测试的概率为


(1)求三人中至少一人通过测试的概率;
(2)设

正确答案
见解析
解析
记甲通过测试为事件


则



------------------2分
(1)设三人中至少有一人通过测试的概率为
率为
所以
(2)

------------------3分
------------------5分


------------------7分

知识点
已知函数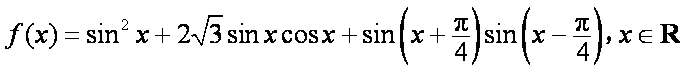
(1)求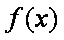
(2)若
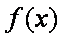
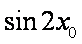
正确答案
见解析。
解析
(1)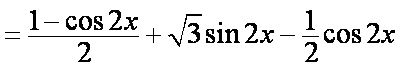
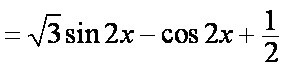
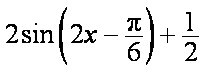
∴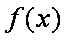
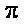
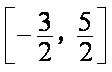
(2)由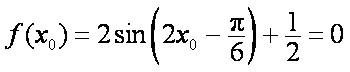
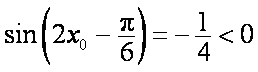
又由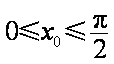
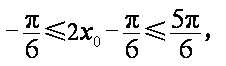
∴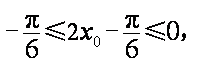
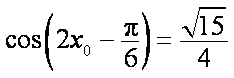
此时,
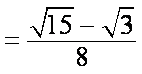
知识点
扫码查看完整答案与解析