- 分布的意义和作用
- 共27题
6. 如图,水平放置的三棱柱ABC-A1B1C1中,侧棱AA1⊥平面A1B1C1,其正视图是边长为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.国家教育部、体育总局和共青团中央曾共同号召,在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日,在全国范围内进行了持续一周的在线调查,随机抽取其中200名大中小学生的调查情况,就每天的睡眠时间分组整理如下表所示:
(Ⅰ)估计每天睡眠时间小于8小时的学生所占的百分比约是多少;
(Ⅱ)该网站利用上边的算法流程图,对样本数据作进一步统计
正确答案
解:(Ⅰ)由样本数据可知,每天睡眠时间小于8小时的频率是

由此估计每天睡眠时间小于8小时的学生约占88%.
(Ⅱ)输入

流程图进入一个求和状态.
设




故输出的S值为6.7.
S的统计意义是指被调查者每天的平均睡眠时间估计为6.7小时.
解析
解析已在路上飞奔,马上就到!
知识点
5.为了了解居民家庭网上购物消费情况,某地区调查了10000户家庭的月消费金额(单位:元),所有数据均在区间
正确答案
750.
解析
由题意得,被调查的10000户家庭中,消费额在1000元以下的户数有:(0.0001+0.00015)×500×10000=750户.
考查方向
解题思路
本题主要考查统计的概念,直方图等知识。解题步骤如下:
找出前面二个矩形的高度,即纵坐标。
利用公式求得结果。
易错点
本题易错点是看不懂直方图中矩形面积的意义,把1000元以下,理解为包含1000元。
知识点
18.某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米.该公司准备从两种户型住宅中各拿出12套销售给内部员工,下表是这24套住宅每平方米的销售价格:(单位:万元/平方米):
根据上表数据,完成下列茎叶图,并分别求出 A,B两类户型住宅每平方米销售价格的中位数;
该公司决定对上述24套住房通过抽签方式销售,购房者根据自己的需求只能在其中一种户型中通过抽签方式随机获取房.号.,每位购房者只有一次抽签机会.
小明是第一位抽签的员工,经测算其购买能力最多为320万元,抽签后所抽得住房价格在其购买能力范围内则确定购买,否则,将放弃此次购房资格.为了使其购房成功的概率
正确答案
(Ⅰ)A户型销售价格的中位数是3,0,B户型销售价格的中位数是4,0,(Ⅱ)该员工选择购买A户型住房的概率大。
解析
(Ⅰ)A户型销售价格的中位数是


若选择B户型抽签,则每平方均价不得高于4.0万元,有能力购买其中的6套住房,所以成功购房的概率是

考查方向
解题思路
解题步骤如下:制作茎叶图,并求出其中位数;根据其购买能力最多为320万元,得出购买 A,B两类户型住宅的最多每平方米的销售价格,容易得出成功购房的概率,比较即可。
易错点
1、本题易在做茎叶图时发生错误。2、本题不容易理解其购买能力最多为320万元,导致无从下手。
知识点
19.在一次数学考试中,数学课代表将他们班
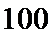
(1)在答题卡上作出这些数据的频率分布直方图;
(2)估计该班学生数学成绩的中位数和平均值;
(3)若按照学生成绩在区间
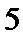
正确答案
(1)见解析;(2)

解析
试题分析:本题属于用样本估计总体与古典概型综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
(Ⅰ)
(Ⅱ)由频率分布直方图可得该班学生数学成绩的中位数为70;
该班学生数学成绩的平均值为
(Ⅲ)由题可得在抽取的5个样本中属于不及格、及格、优良三个等次的个数分别为1、3、1,对应编号分别为

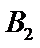


从中任意抽取2名学生的情况有

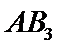
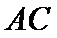





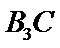
其中至少有一名学生成绩属于及格等次的情况有9种
∴至少有一名学生成绩属于及格等次的概率为
考查方向
解题思路
(1)由表中数据直接绘制直方图;
(2)利用频率分布直方图求中位数和平均值;
(3)用样本的频率代替概率,利用古典概型求概率.
易错点
相关知识点不熟容易处错。
知识点
扫码查看完整答案与解析