几何证明选讲_章节学习

1

题型：单选题

|

单选题 · 5 分

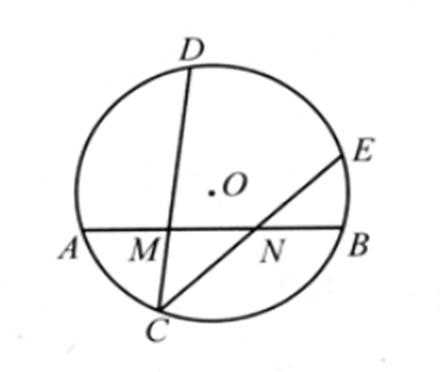
6.如图,在圆O中,M,N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为（）

A

B3

C

D

正确答案

A

解析

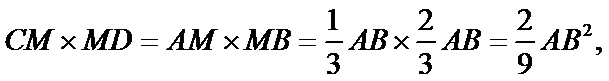
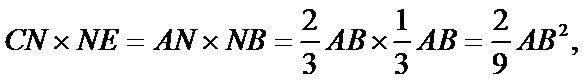
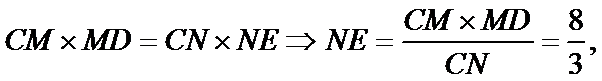
根据相交弦定理可得所以

所以选A.

考查方向

本题主要考查圆中的相交弦定理

解题思路

平面几何中与圆有关的性质与定理是高考考查的热点,解题时要充分利用性质与定理求解,本部分内容中常见的命题点有:平行线分线段成比例定理;三角形的相似与性质;圆内接四边形的性质与判定;相交弦定理与切割线定理.

易错点

相交弦定理的灵活运用

知识点

与圆有关的比例线段

1

题型：简答题

|

简答题 · 10 分

22.如图所示，为半径等于的圆的切线，为切点,交圆于两点，，的角平分线与交于点．

(1)求证；

(2)求的值．

正确答案

（1）见解析；（2）

解析

试题分析：本题属于割线定理及角平分线的性质的问题，1）直接利用三角形相似对应边成比例在化为乘积式即可得到相应的证明；（2）利用角平分线的性质转化为已知线段的比值。

（1）证明：由已知可得,所以可以得到,所以有,即。

（2）由切割线定理可得PB=1，的角平分线与交于点，由角平分线的性质可得,由（1）即可解出。

考查方向

本题考查了几何证明选讲中的利用切割线定理及角平分线的性质的问题。

解题思路

本题考查割线定理及角平分线的性质的问题，解题步骤如下：（1）直接利用三角形相似对应边成比例在化为乘积式即可得到相应的证明；（2）利用角平分线的性质转化为已知线段的比值。

易错点

第2问不会转化要求的比值。

知识点

圆的切线的判定定理的证明圆的切线的性质定理的证明与圆有关的比例线段

1

题型：简答题

|

简答题 · 10 分

22.已知四边形ABCD内接于⊙O，AD：BC=1：2，BA、CD的延长线交于点E，且EF切⊙O于F．

（Ⅰ）求证：EB=2ED；

（Ⅱ）若AB=2，CD=5，求EF的长．

正确答案

（1）见解析；（2）EF=2。

解析

试题分析：本题属于几何证明选讲中有关线段成比例的定理，

（1）利用三角形相似对应边成比例即可得证；

（2）切割线定理的使用。

考查方向

本题考查了几何证明选讲中有关线段成比例的定理。

解题思路

本题考查几何证明选讲中有关线段成比例的定理，解题步骤如下：

（1）利用三角形相似对应边成比例即可得证；

（2）切割线定理的使用。

易错点

定理不熟。

知识点

与圆有关的比例线段

1

题型：简答题

|

简答题 · 10 分

22．如图5,圆O的直径，P是AB延长线上一点，BP=2 ,

割线PCD交圆O于点C，D，过点P作AP的垂线，交直线AC

于点E，交直线AD于点F.

(Ⅰ) 当时，求的度数；

(Ⅱ) 求的值.

正确答案

（1）；（2）24；

解析

：(Ⅰ) 连结BC，∵AB是圆O的直径 ∴则，-----1分

又，--------------2分

，--------------------------------------3分

∵；-------------4分

(Ⅱ)：由（Ⅰ）知，

∴D、C、E、F四点共圆，---------------------------------6分

∴,-----------------------------------------------------------7分

∵PC、PA都是圆O的割线，∴，------------------------------9分

∴=24. ----------------------------------------------------------------10分

考查方向

本题主要考查直径所对的圆周角是直角，四点共圆，切割线定理等知识，意在考查考生的逻辑推理能力和数形结合能力。

解题思路

第（1）问中找不到与之间的关系；第（2）问无法发现D、C、E、F四点共圆导致不能使用割线定理。

易错点

不会使用第（1）问的结论推导第（2）问；

知识点

圆的切线的性质定理的证明弦切角与圆有关的比例线段

1

题型：简答题

|

简答题 · 10 分

22．如图（8），圆O1与圆O2相交于A、B两点，AB是圆O2的直径，过A点作圆O1的切线交圆O2于点E，并与BO1的延长线交于点P，PB分别与圆O1、圆O2交于C，D两点．

（Ⅰ）求证：PA·PD＝PE·PC；

（Ⅱ）求证：AD＝AE．

正确答案

（1）见解析；（2）见解析

解析

试题分析：本题属于几何证明选讲中的证明问题，

（1）由切割线定理直接证明；（2）直接按照步骤来求。

(1) 分别是⊙O2的割线，

①

又分别是⊙O1的切线与割线，

②

由①，②得

(2)连接AC,DE, ⊙O1的直径，

由（1）知，

AB是⊙O2的直径，

考查方向

本题考查了几何证明选讲中的证明问题。

解题思路

本题考查几何证明选讲中的证明问题，解题步骤如下：

（1）由切割线定理直接证明；

（2）直接按照步骤来求。

易错点

图形看不懂，比较复杂。

知识点

相似三角形的判定相似三角形的性质与圆有关的比例线段

1

题型：简答题

|

简答题 · 10 分

已知点在直径的延长线上，切于点，是的平分线且交于点，交于点．

28.求的度数；

29.若，求的值．

第(1)小题正确答案及相关解析

正确答案

（1）；

解析

（1）∵为的切线，∴，又是的平分线，∴．由，得，

又，∴．

考查方向

本题主要考查圆的切线的性质和三角形相似等知识，意在考查考生的分析转化能力与推理论证能力。

解题思路

先根据弦切角定理得，然后利用角平分线得到进而得即可证明；

易错点

没有发现，导致无法证明；

第(2)小题正确答案及相关解析

正确答案

（2）

解析

（2）∵，∴∴，又，∴．在中，∴．

考查方向

本题主要考查圆的切线的性质和三角形相似等知识，意在考查考生的分析转化能力与推理论证能力。

解题思路

先证明，然后即可根据对应边成比例证明。

易错点

看不出，导致没有思路；

1

题型：简答题

|

简答题 · 10 分

22.如图，为四边形外接圆的切线，的延长线交于点，与相交于点，.

（1）求证：；

（2）若，求的长.

正确答案

（1）见解析；（2）。

解析

试题分析：本题属于几何证明选讲的基本问题，

（1）直接按照步骤来求；

（2）由切割线定理和三角形相似即可求出。

（1）为切线，

（2）已知，由切割线定理

得：，得

又知，所以

所以，所以

考查方向

本题考查了几何证明选讲。

解题思路

本题考查几何证明选讲，解题步骤如下：

（1）直接按照步骤来求；

（2）由切割线定理和三角形相似即可求出。

易错点

切割线定理不会用。

知识点

圆的切线的性质定理的证明与圆有关的比例线段

1

题型：简答题

|

简答题 · 10 分

选修4—1：几何证明选讲

如图，正方形ABCD边长为2，以A为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F，连结BF并延长交CD于点E．

27.求证：E为CD的中点；

28.求EF·FB的值．

第(1)小题正确答案及相关解析

正确答案

见解析

解析

解：（Ⅰ）由题可知是以为圆心，为半径作圆，而为正方形，

∴为圆的切线.

依据切割线定理得.

∵圆以为直径，∴是圆的切线，

同样依据切割线定理得.

故.

∴为的中点.

考查方向

本题考察了圆的切割定理，和直角三角形中的射影定理

解题思路

本题解题思路

1）借助圆的切割定理得出，进而证明第一问

2）借助等面积求解FC,使用射影定理得到第二问

易错点

本题易错cd是两圆的切线，

第(2)小题正确答案及相关解析

正确答案

见解析

解析

解：

（Ⅱ）连结，∵为圆的直径，

∴

由

得

又在中，由射影定理得

考查方向

本题考察了圆的切割定理，和直角三角形中的射影定理

解题思路

本题解题思路

1）借助圆的切割定理得出，进而证明第一问

2）借助等面积求解FC,使用射影定理得到第二问

易错点

本题易错cd是两圆的切线，

1

题型：单选题

|

单选题 · 5 分

A

B

C

D

正确答案

D

知识点

与圆有关的比例线段

1

题型：简答题

|

简答题 · 10 分

22.选修4－1：几何证明选讲

如图，是圆的直径，是弦，的平分线交圆于点，，交的延长线于点，交于点。

（Ⅰ）求证：是圆的切线；

（Ⅱ）若，求的值．

正确答案

见解析

解析

试题分析：本题属于平面几何中的基本问题，题目的难度是容易题。

（Ⅰ）连接，可得，∴

又，∴，又为半径，∴是圆的切线

（Ⅱ）过作于点，连接，则有，

设，则，∴

由可得，又由，

可得

考查方向

本题考查了平面几何的知识，主要涉及直线与圆的位置关系，三角形相似的考查．

解题思路

本题考查平面几何的知识，解题步骤如下：

（1）利用圆的相关定理证明。

（2）利用切割线定理和相交弦定理证明。

易错点

知识点

圆的切线的判定定理的证明与圆有关的比例线段

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点