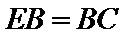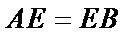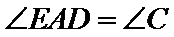- 几何证明选讲
- 共124题
22.如图所示,











(1)求证
(2)求
正确答案
(1)见解析;(2)
解析
试题分析:本题属于割线定理及角平分线的性质的问题,1)直接利用三角形相似对应边成比例在化为乘积式即可得到相应的证明;(2)利用角平分线的性质转化为已知线段的比值。
(1)证明:由已知可得



(2)由切割线定理可得PB=1,





考查方向
解题思路
本题考查割线定理及角平分线的性质的问题,解题步骤如下:(1)直接利用三角形相似对应边成比例在化为乘积式即可得到相应的证明;(2)利用角平分线的性质转化为已知线段的比值。
易错点
第2问不会转化要求的比值。
知识点
正确答案
知识点
选修4-1: 几何证明选讲.
如图所示,已知










28.求证:
29.若

正确答案
证明略
解析
∵



又∵


∴


又∵
考查方向
解题思路
先证明

易错点
找不准三角形相似或全等的条件
正确答案
PA=
解析
∵






∴


∴

考查方向
解题思路
先综合题中条件及28题中结论,解出EP=

易错点
找不准三角形相似或全等的条件
选修4-1:几何证明选讲
如图,过圆













27.求
28.求
正确答案
(1)3;
解析
(Ⅰ)延长




又

又


根据切割线定理得

考查方向
解题思路
1)第一问由切割线定理可得;
2)第二问将两条线段归到两个相似三角形中,用相似得到比例关系。
易错点
三角形相似容易找错,切割线定理用不熟练。
正确答案
(2)
解析
(Ⅱ)过




又由题意知

因此
考查方向
解题思路
1)第一问由切割线定理可得;
2)第二问将两条线段归到两个相似三角形中,用相似得到比例关系。
易错点
三角形相似容易找错,切割线定理用不熟练。
22.如图,ΔOAB是等腰三角形,∠AOB=120°. 以O为圆心,
(Ⅰ)证明:直线AB与⊙O相切;
(Ⅱ)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
正确答案
1
知识点
22.选修4一 1:几何证明选讲如图,直线AB为圆的切线,切点为B,点C


23.选修




24.选修4一 5 


正确答案
22(1)连接DE交BC于点G,由弦切角定理得,
∠ABE=∠BCE, ∠ABE=∠CBE,故∠CBE=∠BCE,
故BE=CE,
又因为DB垂直BE,
所以DE为直径,则∠DCE=90度,
由勾股定理可得,DB=DC
(2)由(1)知,∠CDE=∠BDE,DB=DC,
故DG是BC的中垂线,
所以
连接BO,则∠BOG=60°,从而∠ABE=∠BCE=∠CBE=30°,
所以CF⊥BF,
故Rt△BCF外接圆的半径等于 
23(1)曲线C1的普通方程为
曲线C2的普通方程为
(2)由曲线C1:

所以P点坐标为
由题意可知,M
因此,
所以当


24(1)因为函数定义域为R,所以
设函数

又

所以
故m的取值范围为
(2)由1知m=4
所以
当且仅当

7a+4b有最小值,为
解析
22无 23主要是消去参数。利用解析几何相关知识求解 24先求出函数的最小值,然后确定m的取值范围,第(2)问利用不等式的基本性质转换求解。
考查方向
22主要考查圆切线的性质,相似三角形的计算 23本题主要考查直角坐标和极坐标的相互转换,考察解析几何的简单应用 24本题主要考查不等式的性质与证明
解题思路
22利用线切角定理和勾股定理可证明第一问,第二问做出适当的辅助线即可求解 23消去参数方程中的参数即可,结合三角函数相关性质求得。24利用均值不等式、基本不等式相关性质计算
易错点
22相似度掌握不好计算能力弱 23直角坐标和极坐标不会转换 24对基本不等式掌握不牢
知识点
22.选修4-1:几何证明选讲
如图, 圆M与圆N交于A, B两点, 以A为切点作两圆的切线分别交圆M和圆N于C、D两点,延长DB交圆M于点E, 延长CB交圆N于点F.已知BC=5, DB=10.
(I)求AB的长;
(II)求
正确答案
(1)
(2)
解析
试题分析:本题属于平面几何问题,具体解析如下:
(Ⅰ)根据弦切角定理,
知

∴△


故
(Ⅱ)根据切割线定理,知

两式相除,得
由△



又
由(*)得
考查方向
本题考查了平面几何中圆幂定理的应用,大体可以分成以下几类:
1、圆与圆的位置关系;
2、弦切角定理的应用;
3、相似三角形的判定;
4、切割线定理的应用;
5、相似三角形的性质。
解题思路
本题考查平面几何内圆的相关知识,解题步骤如下:
1、根据弦切角定理判定三角形相似,进而得到AB的值;
2、根据切割线定理得到两边对应成比例,进而得出三角形相似;
3、根据三角形相似的性质,得到比例。
易错点
1、相似三角形的判定应用时条件不全;
2、切割线定理应用时两式相除这个技巧不容易想到;
3、运算出错。
知识点
22.选修4-1:几何证明选讲
如图,点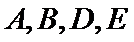






(1)证明:弧

(2)若
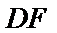
正确答案
(1)见解析;(2)
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
(Ⅰ)证明:∵
∴
∵
∴
∵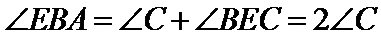
∴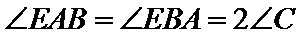
∴
∴
∴
(Ⅱ)由(Ⅰ)知
∴
∴
又∵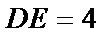
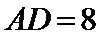
∴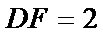
考查方向
解题思路
(1)利用圆的割线的性质及角的关系即可得证;
(2)利用三角形司相似即可求DF的长.
易错点
相关定理不熟悉导致本题失分。
知识点
22.选修4-1:几何证明选讲
如图,












(Ⅰ)求证:

(Ⅱ)若

正确答案
见解析
解析
试题分析:本题属于平面几何中的基本问题,题目的难度是容易题。
(Ⅰ)连接

又




(Ⅱ)过




设

由


可得
考查方向
本题考查了平面几何的知识,主要涉及直线与圆的位置关系,三角形相似的考查.
解题思路
本题考查平面几何的知识,解题步骤如下:
(1)利用圆的相关定理证明。
(2)利用切割线定理和相交弦定理证明。
易错点
相关的定理容易混用。
知识点
请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号。
22.如图AB是圆O直径,AC是圆O切线,BC交圆O与点E。
(1)若D为AC中点,证明:DE是圆O切线;
(2)若

23. 在直角坐标系


(1)求
(2)若直线




24. 已知函数
(1)当

(2)若
正确答案
22.
(1)连接AE,由已知得,AE⊥BC,AC⊥AB.
在Rt△AEC中,由已知得,DE=DC,故∠DEC=∠DCE.
连结OE,则∠OBE=∠OEB
又∠OED+∠ABC=


(2)设CE=1,AE=



所以



23.(1)因为




(2)将




由于


24.(1)当


当

当


当


所以

(2)由题设可得,
所以函数



由题设得

所以

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析