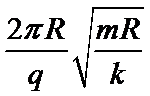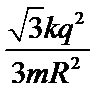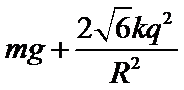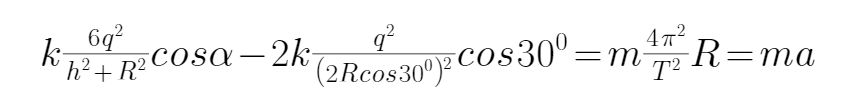- 力的合成与分解的运用
- 共235题
11.如图所示,质量为m的物体A在沿斜面向上的拉力F作用下沿斜面匀速下滑,此过程斜面体B仍静止,斜面体的质量为M,则水平地面对斜面体( )(多选题)
正确答案
解析
ACD.由于A匀速下滑、B静止不动,可将A、B视为整体,根据平衡条件可知,斜面体B应该受到地面对它施加的水平向左的静摩擦力Ff,满足Ff=Fcosθ,竖直方向有:N+Fsinθ=(m+M)g,故AD正确,C错误;
B.对物块A受力分析,物块A受到向上的拉力和向上的滑动摩擦力两者的合力等于mgsinθ,故物块A受的滑动摩擦力大小小于mgsinθ,故B错误;故本题选AD
考查方向
共点力平衡的条件及其应用;力的合成与分解的运用
解题思路
利用整体法对AB组合体进行受力分析,并对拉力F沿水平和竖直两个方向进行正交分解,根据运动状态列方程求解.
易错点
关键应用整体法和隔离体法对物体进行受力分析,根据物体的运动状态列式解答.
教师点评
本题考查了共点力平衡的条件及其应用;力的合成与分解的运用,在近几年的各省高考题出现的频率较高,常与匀变速直线运动规律的综合运用等知识点交汇命题.
知识点
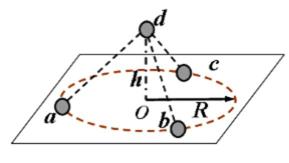
21.如图所示,a、b、c 、d四个质量均为m的带电小球恰好构成“三星拱月”之形,其中a、b、c三 个完全相同的带电小球在光滑绝缘水平面内的同一圆周上绕O点做半径为R的匀速圆周 运动,三小球所在位置恰好将圆周等分。小球d位于O点正上方h处,且在外力F作用下恰处于静止状态,已知a、b、c三小球的电荷量均为q,d球的电荷量为
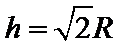
正确答案
解析
A、a、b、c三小球所带电荷量相同,要使三个带电小球做匀速圆周运动,d球与a、b、c三小球一定是异种电荷,由于d球的电性未知,所以a球不一定带正电,故A错误;
BC、设db连线与水平方向的夹角为α,则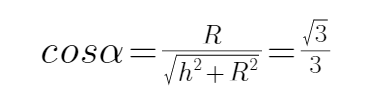
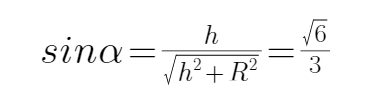
解得: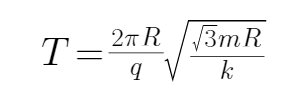
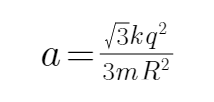
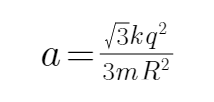
D、对d球,由平衡条件得: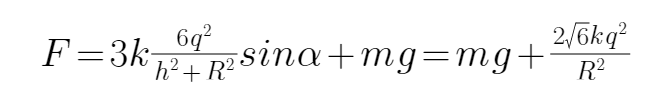
考查方向
电势差与电场强度的关系;库仑定律
解题思路
a、b、c三个带电小球在水平面内做匀速圆周运动,由合外力提供向心力,分析其受力情况,运用牛顿第二定律研究即可.
易错点
关键要正确分析四个小球受力,确定向心力的来源,运用牛顿第二定律和平衡条件研究.
教师点评
本题考查了电势差与电场强度的关系;库仑定律,在近几年的各省高考题出现的频率较高,常与共点力的平衡条件等知识点交汇命题.
知识点
1.如图所示,用一轻绳将质量均匀分布的重球悬挂在竖直光滑的墙上,若将绳子的长度缩短一些,则
正确答案
解析
设绳子和墙面夹角为θ,对小球进行受析:
把绳子的拉力T和墙对球的弹力为N合成,合力为F,由于物体是处于静止的,所以物体受力平衡,物体的重力等于合力F,即F=G,根据几何关系得出:
考查方向
共点力平衡的条件及其应用;力的合成与分解的运用
解题思路
对小球进行受力分析,运用力的合成或分解结合共点力平衡条件列式,当绳子缩短时,即绳子与墙的夹角θ就要变大.
易错点
关键根据平衡条件列出绳子拉力及墙对球的弹力的表达式.
知识点
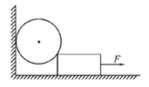
3.如图所示,粗糙的水平地面上的长方形物块将一重为G的光滑圆球抵在光滑竖直的墙壁上,现用水平向右的拉力F缓慢拉动长方体物块,在圆球与地面接触之前,下面的相关判断正确的是 ()
正确答案
解析
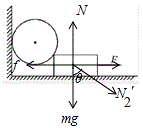
A、对小球和长方形物块整体进行受力分析,整体处于平衡状态,受力平衡,受到重力、地面的支持力、拉力F和墙壁对球水平向右的压力以及水平向左的滑动摩擦力,竖直方向受力平衡,则地面对物块的支持力等于整体的重力,不发生改变,动摩擦因数不变,则滑动摩擦力不变,故AB错误;
C、对长方形物块受力分析,受到重力、地面的支持力、拉力F、球对物块的压力N2′以及滑动摩擦力作用,如图所示:
受力平衡,则水平方向有:
F+N2′sinθ=f,根据牛顿第三定律可知,N2′=N2,由于N2增大,θ增大,f不变,则F减小,故C正确.
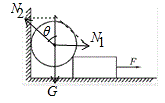
D、对小球进行受力分析,如图所示:
小球受力平衡,则有:N1=Gtanθ,N2=G/cosθ,当水平向右的拉力F缓慢拉动长方体物块时,θ增大,则tanθ增大,所以N1增大,cosθ减小,则N2增大,根据牛顿第三定律可知,球对墙壁的压力逐渐增大,故D错误.
故选:C
考查方向
共点力平衡的条件及其应用.
解题思路
小球受力平衡,对小球进行受力分析,作出受力分析图,当水平向右的拉力F缓慢拉动长方体物块时,θ增大,根据几何关系判断墙对小球的压力和物块对球支持力的大小变化情况,再结合牛顿第三定律判断球对墙壁的压力和球对长木板的压力变化情况,对小球和长方形物块整体进行受力分析,整体处于平衡状态,受力平衡,根据平衡条件及滑动摩擦力公式判断地面对长方体物块的支持力和地面对长方体物块的摩擦力变化情况,再对长方形物块受力分析,根据水平方向受力平衡列式求解水平拉力F的变化情况.
易错点
灵活选择研究对象,并能正确对物体进行受力分析.
知识点
假设某伞兵做跳伞训练,他从悬停在空中的直升机上由静止跳下,跳离直升机一段时间后打开降落伞做减速下落.若他离地面约为100m时迅速打开降落伞,他打开降落伞后的速度图线如图甲所示,降落伞用8根对称的绳悬挂运动员,每根绳与中轴线的夹角均为37°,如图乙所示.已知人的质量为60kg,降落伞质量为10kg,不计打开降落伞前伞兵下落所受的阻力,打开伞后降落伞所受阻力Ff与速度v成正比,即Ff=kv,k为阻力系数,求(取g=10m/s2):
35.打开降落伞瞬间伞兵的加速度a;
36.为安全起见,每根悬绳至少应能承受多大的拉力;
正确答案
a=30m/s2,方向竖直向上
解析
当人和降落伞的速度v=5m/s时做匀速运动,则:
kv=(M+m)g,
解得:k=140N•s/m
对整体,根据牛顿第二定律得:
kv0-(M+m)g=(M+m)a,
代入数据解得:a=30m/s2,方向竖直向上
考查方向
牛顿运动定律的综合应用
解题思路
根据人和降落伞一起做匀速运动时,结合此时的速度,根据共点力平衡求出阻力系数.对整体分析,根据牛顿第二定律求出打开伞瞬间的加速度a的大小和方向;
易错点
通过图线能够得出人和降落伞的运动规律,结合共点力平衡和牛顿第二定律进行求解.
正确答案
T=375N
解析
设每根绳拉力为T,以运动员为研究对象有:
8Tcos30°-(M+m)g=(M+m)a,
T≈375N
由牛顿第三定律得:悬绳能承受的拉力至少为375N.
考查方向
牛顿运动定律的综合应用
解题思路
当加速度最大时,绳子的拉力最大,根据牛顿第二定律求出拉力.
易错点
通过图线能够得出人和降落伞的运动规律,结合共点力平衡和牛顿第二定律进行求解.
扫码查看完整答案与解析