对数的运算性质
共69题

· 对数的运算性质

对数的运算性质
共69题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

5.设函数f(x)=，则f (－2)+ f (log212) =( )

D12

正确答案

知识点

函数的值对数的运算性质

题型：填空题

填空题 · 4 分

12.若，则．

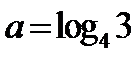
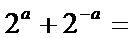
正确答案

；

解析

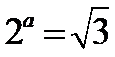
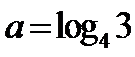
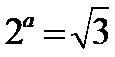
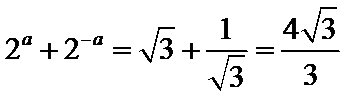
试题分析：根据指数式与对数式的关系求出，然后代入求值。

∵，∴，即，∴。

考查方向

本题考查了对数的运算，对数式与指数式的关系，属于基础题．

解题思路

由可得出，然后代入进行求值即可．

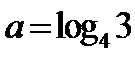
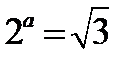
易错点

要正确应用指数的运算法则.

知识点

对数的运算性质

题型：单选题

单选题 · 5 分

4．设，，，则a, b, c的大小顺序是（）

正确答案

解析

因为，，又在R上单调递增，且恒大于零，所以，而，所以，故选C.

考查方向

本题主要考查了指数、对数的基本运算以及指数函数的单调性，在近几年的各省高考题出现的频率也较高。

解题思路

先分别的取值范围，比较即可。

易错点

本题易在比较a, b时出错。

知识点

指数幂的运算对数的运算性质

题型：单选题

单选题 · 5 分

1．设集合，，则

正确答案

解析

集合A中的不等式可化为

，则有，

则

A选项不正确，B选项不正确，C选项不正确，所以选D选项。

考查方向

本题主要考查了集合的交集运算及指数不等式、对数不等式的求解能力，并涉及了对数函数的定义域问题。

解题思路

分别求解不等式得到，

再借助数轴进行交集运算，即可得到结果。

A选项不正确，B选项不正确，C选项不正确，所以选D选项。

易错点

如何把不等号两边化为“同底”

解对数不等式时忽略了真数大于0

知识点

交集及其运算指数幂的运算对数的运算性质

题型：单选题

单选题 · 5 分

若，则的最小值是（）

正确答案

解析

由化同底得：

两边同时除以得：，要使对数有意义知均为正数，由均值不等式：，当且仅当“”时，取“=”号。故选D选项。

考查方向

本题主要考查了对数运算和均值不等式,在近几年的各省高考题出现的频率较高，属于难题。

解题思路

1、由得到的等量关系；2、由均值不等式求出的最小值。

易错点

1、本题易在对数运算上卡住，难以得到的等量关系； 2、对均值不等式的结构不熟悉导致解题出错；

知识点

对数的运算性质利用基本不等式求最值

题型：单选题

单选题 · 5 分

4．设，，，则a, b, c的大小顺序是（）

正确答案

解析

因为，，又在R上单调递增，且恒大于零，所以，而，所以，故选C.

考查方向

本题主要考查了指数、对数的基本运算以及指数函数的单调性，在近几年的各省高考题出现的频率也较高。

解题思路

先分别的取值范围，比较即可。

易错点

本题易在比较a, b时出错。

知识点

指数幂的运算对数的运算性质

题型：填空题

填空题 · 5 分

14．已知,那么的值是．

正确答案

解析

由题可知，将展开的两式相加减，可求出tana/tanb=5，代入对数式得值为1．

考查方向

本题主要考查了两角和差公式及对数运算

解题思路

本题考查两角和差公式及对数运算，解题思路如下：

1、利用两角和差公式展开已知，两式相加减，求出正切值；

2、代入对数式求解。

易错点

本题必须注意两角和差公式

知识点

对数的运算性质两角和与差的正弦函数

题型：填空题

填空题 · 4 分

（4分）（2015•上海）方程log2（9x﹣1﹣5）=log2（3x﹣1﹣2）+2的解为　　　　　　．

正确答案

知识点

对数的运算性质

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 换底公式的应用

百度题库 > 高考 > 理科数学 > 对数的运算性质

扫码查看完整答案与解析