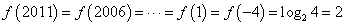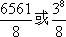· 函数的基本性质

· 求函数的值

求函数的值
共92题

· 函数的基本性质

· 求函数的值

求函数的值
共92题

热门试卷

X 查看更多试卷

1

题型：简答题

|

简答题 · 12 分

已知函数的极大值点为。

（1）用实数来表示实数，并求的取值范围；

（2）当时，的最小值为，求的值；

（3）设，两点的连线斜率为，求证：必存在

，使。

正确答案

见解析。

解析

（1），由题设知。

由韦达定理得另一极值点，因为为极大值点，

故。

（2）上递增，在递减，在上递增，

故当时，分情况如下：

当，即时，在上单调递减；

，解得，不合条件，舍去。

当，即时，

，化简得，取，故所求的。

（3），即证。

即证方程在上有实数解。

记，。

当，

即或时，由零点存在定理知此时方程有解。

当时，此时，，且二次函数的

对称轴，由此可知此时方程在内有两个解；

当时方程有一根为，当时方程有一根为。

综上可知，方程在上有实数解。

知识点

求函数的值

1

题型：单选题

|

单选题 · 5 分

若函数，则（其中为自然对数的底数）

A

B

C

D

正确答案

C

解析

略

知识点

求函数的值

1

题型：单选题

|

单选题 · 5 分

已知= 则等于（）

A–1

B0

C1

D2

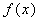
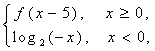
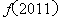
正确答案

D

解析

知识点

求函数的值

1

题型：填空题

|

填空题 · 4 分

设是定义在上的函数，若，且对任意的，满足，则=____________。

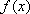
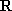
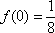
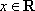
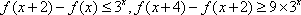
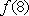
正确答案

解析

略

知识点

抽象函数及其应用求函数的值由其它方法求数列的通项公式

1

题型：填空题

|

填空题 · 5 分

已知函数,点P()在函数图象上，那么的最小值是____________.

正确答案

4

解析

略

知识点

求函数的值

继续学习学习下一知识点

下一知识点 : 函数恒成立、存在、无解问题

百度题库 > 高考 > 文科数学 > 求函数的值

扫码查看完整答案与解析