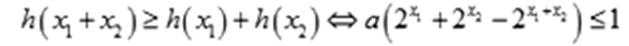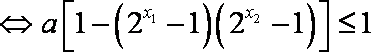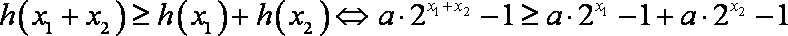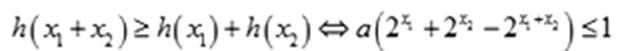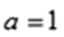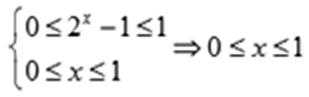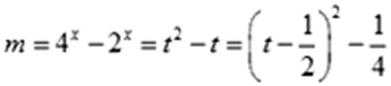- 函数恒成立、存在、无解问题
- 共23题
已知函数f (x)的导数f(x)满足0<f(x)<1,常数a为方程f (x)=x的实数根。
(1)若函数f (x)的定义域为M,对任意[a,b]M,存在x0[a,b],使等式
f (b)–f (a)=(b–a)f(x0)成立,求证:方程f (x)=x存在唯一的实数根a;
(2)求证:当x>a时,总有f (x)<x成立;
(3)对任意x1、x2,若满足|x1–a|<2,|x2–a|<2,求证:|f (x1)–f (x2)|<4.
正确答案
见解析。
解析
知识点
已知向量





(1)求实数
(2)若不等式


正确答案
(1)
解析
(1)由题得
又



(2)由(1)的他,
令



即





知识点
设曲线






(1)求
(2)求函数
(3)求证:
正确答案
见解析。
解析
(1)



(2)


又

(3)证明:
∴原式





知识点
对定义在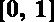
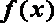
① 对任意的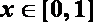
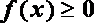
② 当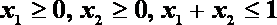
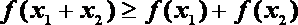
已知函数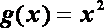
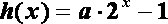
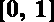
(1)试问函数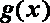
(2)若函数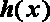
(3)在(2)的条件下,若方程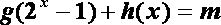
正确答案
见解析
解析
(1)当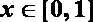
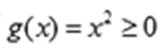
当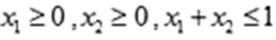
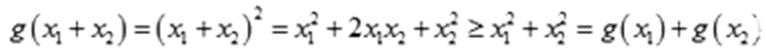
所以函数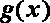
(2)因为函数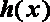
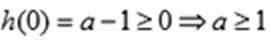
根据②有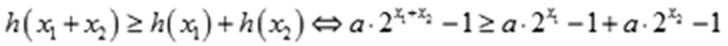
因为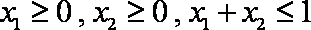
所以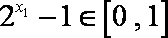
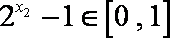
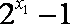
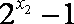
于是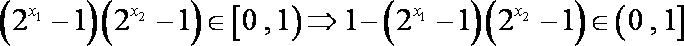
所以
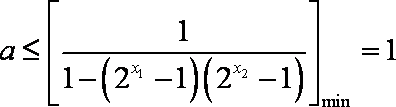
于是
另解:因为函数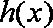
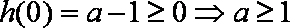
根据②有
取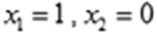
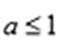
(3)根据(2)知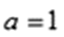

由
令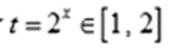
因此,当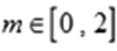
知识点
23.已知函数



(1)求
(2)问:是否存在边长为







(3)若函数




正确答案
(1)把

可得:
化简此方程组可得:
即
可得

代入原方程组可得:
(2)由

此三角形的高即点






即





直线
即
(3)由题意知:












又


解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析