- 向量的加法及其几何意义
- 共68题
3.已知向量





正确答案
知识点
13.已知向量a=(m,4),b=(3,-2),且a∥b,则m=___________.
正确答案
-6
解析
因为a∥b,所以

考查方向
解题思路
如果a=(x1,y1),b=(x2,y2)(b≠0),则a∥b的充要条件是x1y2-x2y1=0.
易错点
a∥b的充要条件容易与垂直混淆或错记。
知识点
已知向量
正确答案
知识点
13.已知向量a=(1,–1),b=(6,–4).若a⊥(ta+b),则实数t的值为________.
正确答案
-5
解析
由已知条件可得



考查方向
解题思路
根据两向量垂直,数量积为0结合数量积的坐标运算得出t为变量的方程,得解.
易错点
向量垂直的一般处理思路是两向量的数量积为0。
知识点
13.已知平面向量





正确答案
解析
因为




所以
所以
其中
所以当


考查方向
解题思路
本题考查分析转化能力.设向量




易错点
辅助角公式的正确运用
知识点
5.设

①若

②若

③若


④若

其中真命题的个数是
正确答案
解析
第1个,两直线也可能为异面直线,故错误,第2个正确,第三个也可能是m在平面呢,故错误,第4个比如正方体的相邻的三个面,就是反例,所以真命题只有1个,所以选B
考查方向
解题思路
根据直线与平面的位置关系的特征,逐一判断
易错点
考虑直线和平面位置关系考虑不周全
知识点
9.已知向量
正确答案
解析

考查方向
解题思路
利用向量夹角公式进行计算
易错点
要选用向量夹角的坐标公式
知识点
13.在正六边形
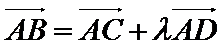

正确答案
解析
试题分析:依题意可知


考查方向
解题思路
直接运用向量的运算律进行计算。
易错点
对向量的运算率不熟悉导致出错。
知识点
扫码查看完整答案与解析