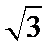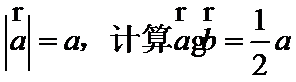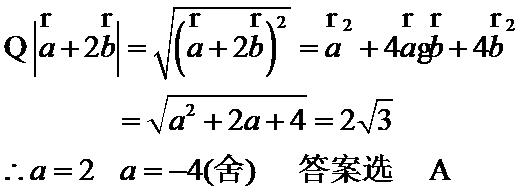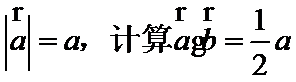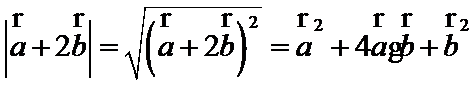- 数量积表示两个向量的夹角
- 共88题
1
题型:
单选题
|
5.已知平面向量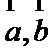
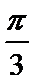
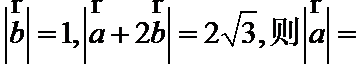
正确答案
A
解析
由题意得设
考查方向
本题主要考察了向量的数乘,考察了向量的数量积运算,属于简单题
解题思路
本题属于基本概念题,使用直接法,
1、由题意得设
2、根据数量积的性质
3、带入计算可得结果,注意a的范围
易错点
该题出错在计算错误
知识点
数量积表示两个向量的夹角
1
题型:填空题
|
14.已知平面向量



正确答案
解析

考查方向
本题主要考察了向量的减法及其几何意义,考察了向量的三角形法则,考察了正弦定理,该题比较综合,属于中档题
解题思路
1)根据题意使用有向线段表示向量,并构造三角形
2)利用三角形的正弦定理得出
3)根据角的取值范围得到取值范围
易错点
本题易错在无法找到有效的解题思路
知识点
平面向量数量积的运算数量积表示两个向量的夹角
1
题型:填空题
|
13.已知向量




正确答案
解析
由已知得


考查方向
本题主要考查了平面向量的垂直、数量积问题,考查考生的运算能力。
解题思路
要求





易错点
不能理解什么样的向量可作基底。
知识点
平面向量数量积的运算数量积表示两个向量的夹角
1
题型:简答题
|
已知向量


17.求向量

18.求
第(1)小题正确答案及相关解析
正确答案
解析
∵
又
∴
即
解得
又
所以

考查方向
本题考查平面向量数量积的运算及其定义,解题的关键是根据题设条件解出两向量的内积及掌握平方法求向量的模
解题思路
由题意,可根据题中条件求出
的夹角;
易错点
要区分点的坐标和向量的坐标,向量坐标中包含向量大小和方向两种信息;两个向量共线有方向相同、相反两种情况。
第(2)小题正确答案及相关解析
正确答案
解析

考查方向
本题考查平面向量数量积的运算及其定义,解题的关键是根据题设条件解出两向量的内积及掌握平方法求向量的模
解题思路
先对
易错点
求向量模的常用方法:利用公式
下一知识点 : 量积判断两个平面向量的垂直关系
扫码查看完整答案与解析