- 函数恒成立问题
- 共47题
21.已知:函数


(1)求a的值
(2)若

(3)讨论关于x的方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)求证:
(2)当




正确答案
(1)
依题意

(2)






即
考虑函数



所以



由




解析
解析已在路上飞奔,马上就到!
知识点
21.已知





(1)若


(2)设





正确答案
(1)“







(2) 当
对任意






由


解析
解析已在路上飞奔,马上就到!
知识点
12.已知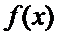
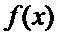
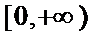
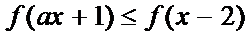
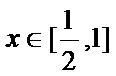
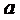
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.已知函数




(1)判断函数

(2)若


(3)若定义域为









正确答案
解:(1)若



即


因此

若



即存在常数对


(2)


则
当

因此

则有
即
即
当


因此满足


(3) 函数



于是
即



因此
综上可知当


解析
解析已在路上飞奔,马上就到!
知识点
10.已知R上的连续函数g(x)满足:
①当



②对任意的






若关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设函数













正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知












①
②
③
④
则在区间

正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
22.设

(1)当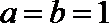

(2)设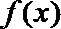


(3)当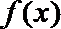
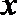

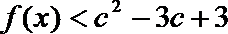
正确答案
(1)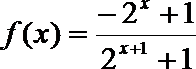

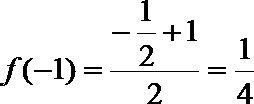
所以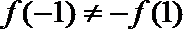
因此,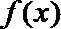
(2)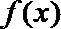
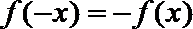
即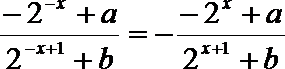
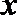
化简整理得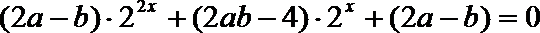
这是关于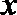

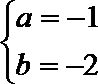
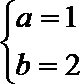
(3)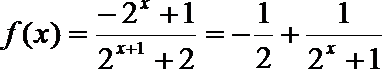
因为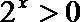
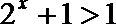
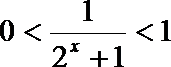

而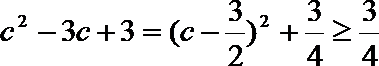
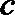
所以对任何实数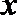
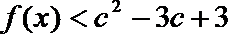
解析
解析已在路上飞奔,马上就到!
知识点
17.若函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析