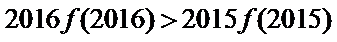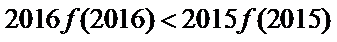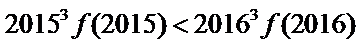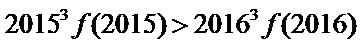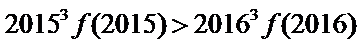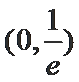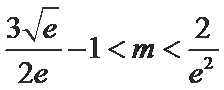- 函数恒成立问题
- 共47题
9.已知一次函数





正确答案
解析
f(0)=-1;f(1)=a-1, 使得



考查方向
解题思路
由于是直线型函数,求两个端点值,f(1)=a-1<0,解得 a
易错点
对于恒成立问题理解错,数形结合应用。
知识点
12.已知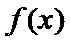
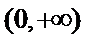
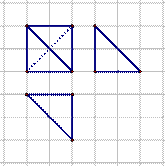
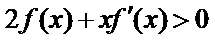
正确答案
解析
构造函数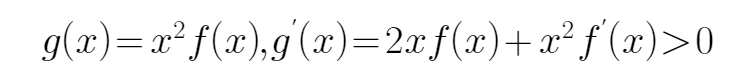
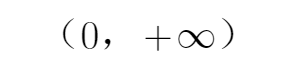
集合不等式的性质,选D
考查方向
利用导数判断函数的单调性和单调区间
解题思路
先构造函数,然后求导,然后判断单调性进而证明不等式
易错点
构造不出来正确的函数
教师点评
解决此类问题关键在于构造正确的函数,而构造函数在于对一些式子有“敏感度”学生要多做相关题型的题,总结经验
知识点
已知函数
25.当

26.当


正确答案
详见解析
解析
令



故
考查方向
利用导数证明不等式,导数和函数相结合问题
解题思路
先求导,然后判断函数的单调性,构造恰当的函数,证明不等式
易错点
不能正确的构造出函数,求导错误
正确答案
详见解析
解析
当


当

所以

令
令
当

令




因此


所以,当

当

令




因此,


所以,当

综上,当



考查方向
利用导数证明不等式,导数和函数相结合问题
已知不等式成立求参数的取值范围
解题思路
求导,分类讨论,然后判断函数单调性
根据不等式成立,求参数的取值范围
易错点
计算能力弱,分类讨论有重复或有遗漏
正确答案
LUE
知识点
正确答案
略
知识点
物业管理保安服务的目的是指为维护物业管理区域内的公共秩序而( )。
A.实施的正当防卫活动
B.实施的紧急避险活动
C.配合公安机关实施的社会综合治安的安全防范活动
D.实施的安全保障职能的活动
正确答案
C
解析
暂无解析
设函数f(x)=ax2+b,其中a,b是实数.
20.若ab>0,且函数f[f(x)]的最小值为2,求b的取值范围;
21.求实数a,b满足的条件,使得对任意满足xy=l的实数x,y,都有f(x)+f(y))≥f(x)f(y))成
立.
正确答案
详见解析
解析
考查方向
函数的综合题,二次函数的性质和特征
已知函数的最值求参数的取值范围
解题思路
根据题意化简成二次函数,然后利用二次函数的性质求其最值
易错点
化简错误,分类讨论出错
正确答案
详见解析
解析
考查方向
平均值不等式
不等式与函数的综合应用
解题思路
根据所给函数的性质,求出a、b之间的关系,然后化简等式,构造出平均值不等式的形式,最后求出满足的条件
易错点
化简错误,不能想到用平均值不等式求解
在某钢材公司诉某建筑公司偿还5万元欠款一案中,钢材公司不服法院一审判决并通过一审法院提出上诉,在二审法院尚未接到案件之前,钢材公司见建筑公司转移财产,向法院申请采取财产保全。后法院扣押了建筑公司的一批建筑设备(价值万元)。有关该案的下列说法正确的是( )。
A.应当由第一审人民法院采取财产保全措施
B.在二审审理的过程中,即使建筑公司提供担保,二审法院也无权解除财产保全,必须由一审人民法院采取解除措施
C.法院扣押建筑公司建筑设备(价值7万元)的措施并无任何不妥
D.如果建筑公司对财产保全不服,则可以向法院申请复议,复议期间停止财产保全的执行
正确答案
A
解析
[考点] 财产保全 [解析] 本题考查的是财产保全制度。《民诉意见》第103条规定:对当事人不服一审判决提出上诉的案件,在第二审人民法院接到报送的案件之前,当事人有转移、隐匿、出卖或者毁损财产等行为,必须采取财产保全措施的,由第一审人民法院依当事人申请或依职权采取。第一审人民法院制作的财产保全裁定,应及时报送第二审人民法院。本案中,钢材公司是在通过一审法院上诉后、二审法院没有收到案件前提出的财产保全申请,所以应当由一审法院采取措施。A选项正确。 《民事诉讼法》第95条规定:被申请人提供担保的,人民法院应当解除财产保全。所以,如果建筑公司提供担保,则应当解除财产保全。《民诉意见》第108条规定:人民法院裁定采取财产保全措施后,除作出保全裁定的人民法院自行解除和其上级人民法院决定解除外,在财产保全期限内,任何单位都不得解除保全措施。由此可知,有权解除财产保全的是作出裁定的人民法院以及其上级人民法院。根据A选项可知,本案中作出财产保全裁定的是一审法院,所以一审法院和二审法院都有权解除财产保全。B选项不正确。 《民事诉讼法》第94条第1款规定:财产保全限于请求的范围,或者与本案有关的财物。本案当事人的诉讼请求是5万元,而法院财产保全的财产价值为7万元,超出了法定财产保全的范围。C选项不正确。 《民事诉讼法》第99条规定:当事人对财产保全或者先予执行的裁定不服的,可以申请复议一次。复议期间不停止裁定的执行。所以,如果建筑公司对财产保全不服可以申请复议,但复议期间不停止财产保全的执行。D选项不正确。
已知函数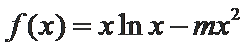
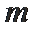
25.当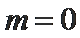
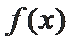
26.若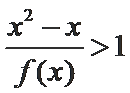
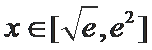
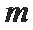
27.若
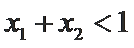
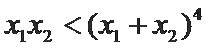
正确答案
当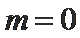
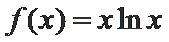
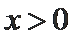
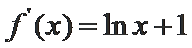
由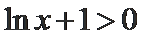
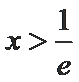
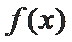
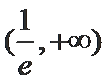
由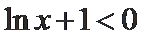
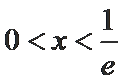
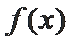
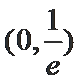
∴综上,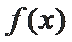
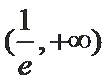
解析
当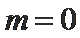
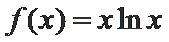
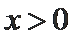
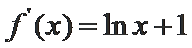
由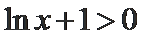
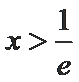
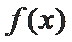
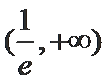
由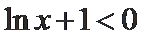
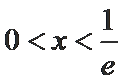
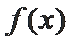
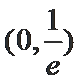
∴综上,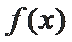
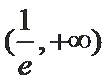
考查方向
本题主要考查了导数的应用——利用导数求函数的单调区间问题,属于常规性问题。
解题思路
首先将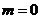
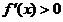
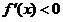
易错点
本题容易因含有对数的超越不等式不会解而导致结果算不出来。
教师点评
本题属于常规性问题,在每一年的高考中都会考到,需要考生加强这一类问题的训练。
正确答案
已知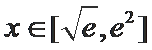
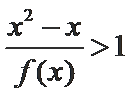
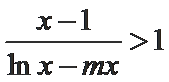
从而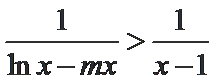
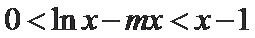
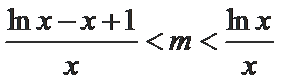
令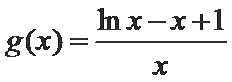
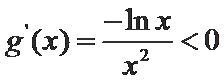
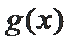
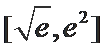
∴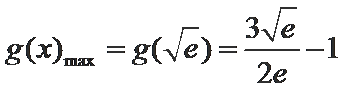
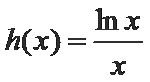
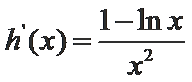
当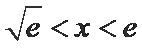
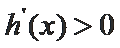
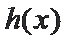
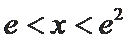
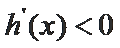
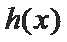
而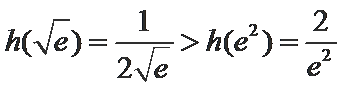
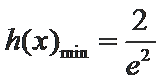
解析
已知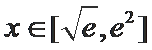
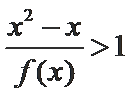
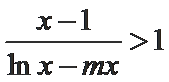
从而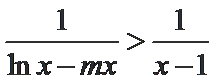
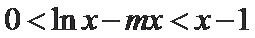
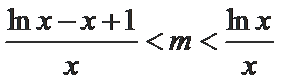
令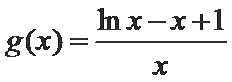
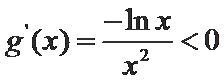
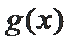
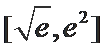
∴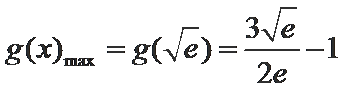
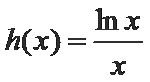
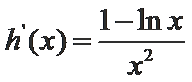
当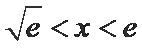
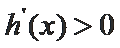
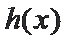
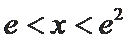
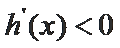
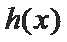
而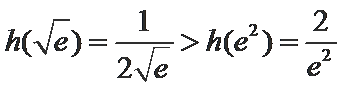
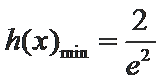
考查方向
本题主要考查了导数的应用,通过求最值来解决不等式恒成立的问题。
解题思路
首先将问题转化为求函数的最值的问题,然后在利用导数予以解决。
易错点
本题在对恒成立问题的分析中容易产生错误的理解而导致出错。
正确答案
由(1)知,当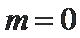
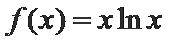
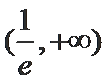
∵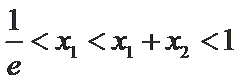
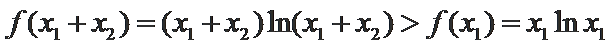
即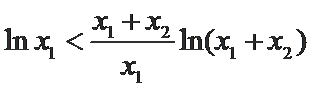
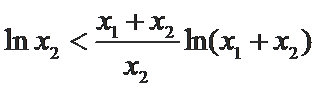
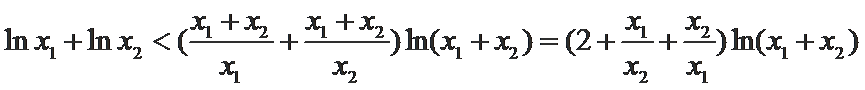
又因为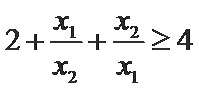
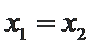
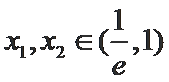
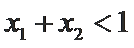
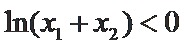
∴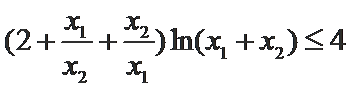
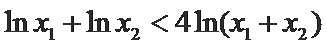
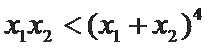
解析
由(1)知,当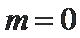
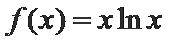
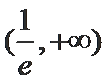
∵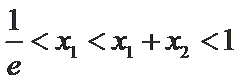
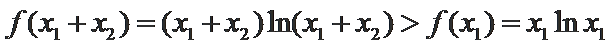
即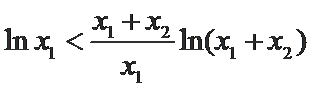
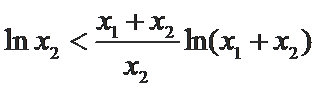
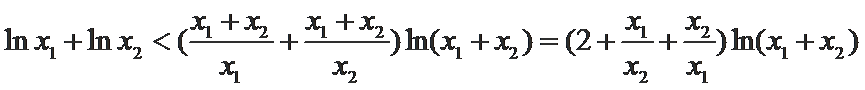
又因为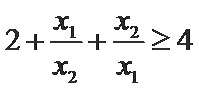
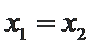
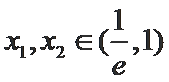
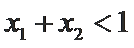
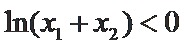
∴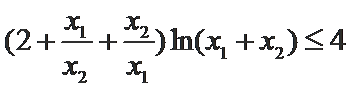
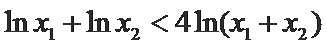
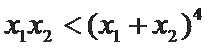
考查方向
本题考查了导数的应用以及不等式的证明。
解题思路
首先根据函数的单调性予以放缩,再利用放缩法予以证明。
易错点
本题容易因为放缩法掌握不清楚而导致出现错误。
教师点评
本题属于不等式的证明问题,难度较大,考生需要有足够的知识储备和应变能力。
扫码查看完整答案与解析