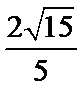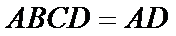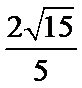- 直线、平面垂直的综合应用
- 共65题
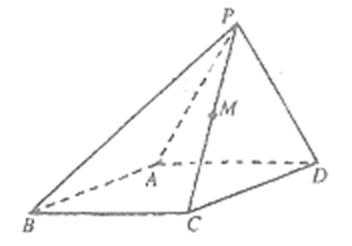
如图





21.证明:

22.证明:
23.求点

正确答案
(1)证明见解析;
解析
(1)因为四边形






考查方向
解题思路
(1)由四边形




















易错点
定理的条件不完整,书写格式不规范。
正确答案
(2)证明见解析;
解析
(2)因为四边形











考查方向
解题思路
(1)由四边形




















易错点
定理的条件不完整,书写格式不规范。
正确答案
(3)
解析
(3)取































考查方向
解题思路
(1)由四边形




















易错点
定理的条件不完整,书写格式不规范。
如图,四棱锥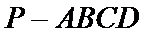
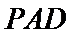
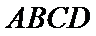
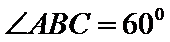
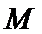
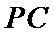
22.求证: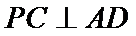
23.求点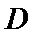
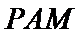
正确答案
(1)略;
解析
(1):取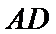
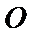
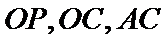
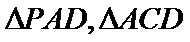
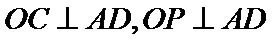
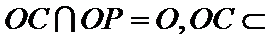
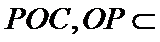
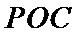
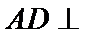
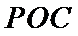
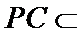
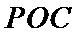
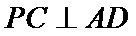
考查方向
解题思路
先证明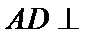
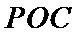
易错点
不会做辅助线导致没有思路;
正确答案
(2)
解析
(2)点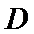
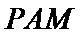
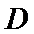
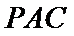
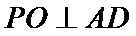
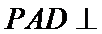
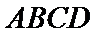
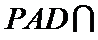

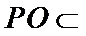
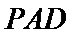
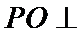
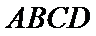
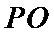
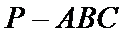
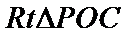
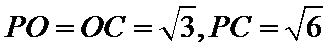
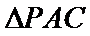
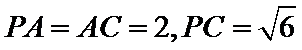
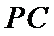
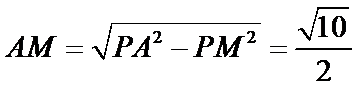
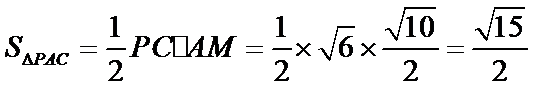
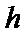
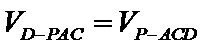
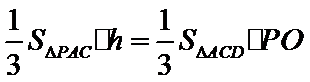
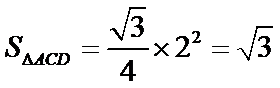
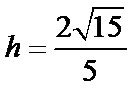
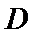
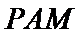
考查方向
解题思路
先发现点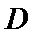
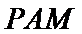
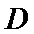
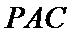
易错点
看不出点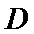
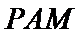
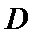
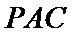
19. 如图,在矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
(Ⅰ)若E为BD的中点,求证:
正确答案
(1)见解析;(2)
解析
试题分析:本题属于立体几何的证明与体积的计算问题,
(1)由已知条件然后结合线面平行的判定定理来证明;
(2)将底面换了之后再来计算其体积。
(1)证明:取



又






(2)在平面图形




考查方向
解题思路
本题考查立体几何的证明与体积的计算问题,解题步骤如下:
(1)由已知条件然后结合线面平行的判定定理来证明;
(2)将底面换了之后再来计算其体积。
易错点
不会换底去计算体积。
知识点
4.设



正确答案
解析
试题分析:根据线面垂直,线面平行,面面平行的关系逐个进行判断。
对于A,∵l⊥



对于B,当



对于C,当l∥



对于D,当



考查方向
解题思路
A根据线面垂直的判定定理得出A正确;B根据面面垂直的性
质判断B错误C根据面面平行的判断定理得出C错误;D根据面面平行的性质判断D错误.
易错点
要考虑到空间直线,平面可能出现的各种关系.
知识点
11.如图,网格纸上小正方形的边长为
某几何体的三视图,则该几何体最长的棱长等于
正确答案
解析
该几何体为三棱锥,其棱长分别为:
知识点
扫码查看完整答案与解析