- 不等式
- 共1175题
13．已知不等式组
正确答案
6
解析
解析已在路上飞奔，马上就到！
知识点
11． 设不等式组
正确答案
[0，8]
解析
解析已在路上飞奔，马上就到！
知识点
11．如果实数
正确答案
5
解析
解析已在路上飞奔，马上就到！
知识点
2．已知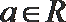
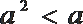
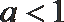
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．
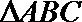
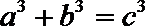
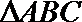
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6． 若实数x，y满足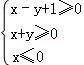
A0
B1
C
D9
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．已知
正确答案
4
解析
解析已在路上飞奔，马上就到！
知识点
15．在等式
正确答案
30
解析
解析已在路上飞奔，马上就到！
知识点
6．若实数
A0
B1
C
D9
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．设变量x、y满足
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．已知
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
20．解下列不等式：
（1）|x﹣1|+|x﹣2|＜2；
（2）0＜x﹣
正确答案
解：（1）∵ 数轴上0.5与2.5到1与2的距离均为2，
∴ 由|x﹣1|+|x﹣2|＜2，得
∴ 原不等式的解集为{x|
（2）∵ 0＜x﹣
∴
解①得：﹣1＜x＜0或x＞1；
解②得：x＜
综合①②得，﹣1＜x＜
解析
解析已在路上飞奔，马上就到！
知识点
7．已知不等式组
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．不等式
正确答案
（-2，2）
解析
解：由题意，考察y=
∵ 
∴ x2+ax＞2x+a﹣2恒成立
∴ x2+（a﹣2）x﹣a+2＞0恒成立
∴ △=（a﹣2）2﹣4（﹣a+2）＜0
即（a﹣2）（a﹣2+4）＜0
即（a﹣2）（a+2）＜0
故有﹣2＜a＜2，即a的取值范围是（﹣2，2）
故答案为（﹣2，2）
知识点
13．已知P1（x1，x2），P2（x2，y2）是以原点O为圆心的单位圆上的两点，∠P1OP2=θ（θ为钝角）．若sin（
正确答案
解析
由题意可得
∴ 
∴ 
∴ cosθ=﹣
∴ 
知识点
扫码查看完整答案与解析