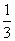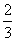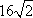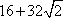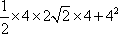- 立体几何与空间向量
- 共2637题
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
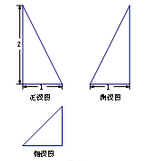
某三棱锥的三视图如图所示，则该三棱锥的体积是
A
B
C
D1
正确答案
解析
由三视图可看出该三棱锥的底面为直角边为1的等腰直角三角形，高为2，所以该三棱锥的体积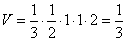
知识点
将正方形（如图1所示）截去两个三棱锥，得到图2所示的几何体，则该几何体的左视图为 （ ）
A
B
C
D
正确答案
解析
因为从左面垂直光线在竖直平面上的正投影是正方形，其中
知识点
一几何体的三视图如图所示，则该几何体的体积为
正确答案
解析
还原后的直观图是一个长宽高依次为10，6 ，5的长方体上面是半径为3高为2的半个圆柱。
知识点
如图，正方体的底面与正四面体的底面在同一平面α上，且AB//CD,则直线EF与正方体的六个面所在的平面相交的平面个数为 。
正确答案
4
解析
设CD的中点为M，连结EM，FM易证平面EFM
知识点
实部为
正确答案
解析
由已知复数对应的坐标为
知识点
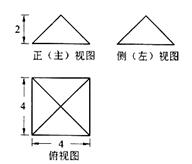
某四棱锥的三视图如图所示，该四棱锥的表面积是( )。
A32
B16+
C48
D
正确答案
解析
由三视图可知几何体为底面边长为4，高为2的正四
棱锥，则四棱锥的斜高为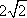
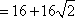
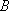
知识点
已知某几何体的三视图如图所示，则该几何体的体积为______。
正确答案
12π
解析
该几何体是由3个圆柱构成的几何体，故体积V＝2×π×22×1＋π×12×4＝12π
知识点
若一个几何体的三视图如图所示，则此几何体的体积为( )
A
B5
C
D4
正确答案
解析
由三视图可判断该几何体为直六棱柱，其底面积为4，高为1，所以体积为4，故选D项
知识点
一个四面体的顶点在空间直角坐标系O－xyz中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为( )。
A
B
C
D
正确答案
解析
如图所示，该四面体在空间直角坐标系O－xyz的图像为下图：
则它在平面zOx的投影即正视图为
知识点
某四棱锥的三视图如图所示，则最长的一条侧棱长度为（ ）
A
B
C
D
正确答案
解析
略
知识点
四棱锥
则四棱锥
A24
B18
C
D8
正确答案
解析
略
知识点
已知某几何体的三视图，根据图中标出的尺寸 （单位：
A
B
C
D
正确答案
解析
由三视图可知，该几何体为底面是正方形，且边长为2cm，高为2cm的四棱锥，
如图，
故
故选B。
知识点
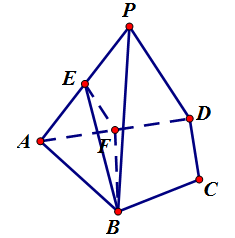
如图，在四棱锥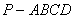
求证：（1）直线EF∥平面PCD；
（2）平面BEF⊥平面PAD
正确答案
见解析
解析
证明：（1）在△PAD中，因为E、F分别为
AP，AD的中点，所以EF//PD.
又因为EF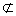
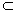
所以直线EF//平面PCD.
（2）连结DB，因为AB=AD，∠BAD=60°，
所以△ABD为正三角形，因为F是AD的
中点，所以BF⊥AD.因为平面PAD⊥平面
ABCD，BF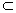
知识点
某几何体的三视图如图所示，则该几何体的体积为( )。
正确答案
解析
该几何体为一个半圆柱与一个长方体组成的一个组合体。
V半圆柱＝
V长方体＝4×2×2＝16.
所以所求体积为16＋8π.故选A.
知识点
扫码查看完整答案与解析