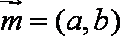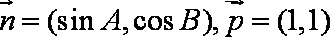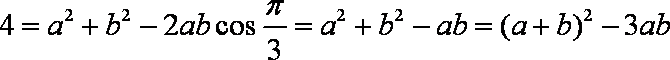- 幂函数的概念、解析式、定义域、值域
- 共682题
已知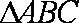
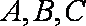
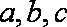
(1)若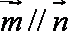
(2)若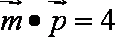
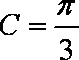
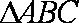
正确答案
见解析。
解析
(1) 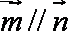
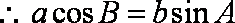
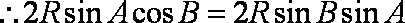
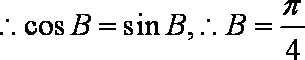
(2)由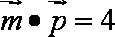
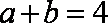
由余弦定理可知:
于是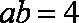
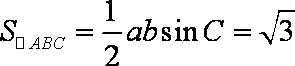
知识点
已知:


(1) 求


(2) 若


正确答案
见解析。
解析
(1)



(2) ∵

∴当



∵
∴
知识点
已知数列
(1) 求数列

(2) 求数列


正确答案
见解析。
解析
(1)由已知

由已知
设等比数列


(2)设数列
则
两式相减得



知识点
在




(1)求函数
(2)求
正确答案
见解析。
解析
(1)



应用正弦定理,知


(2)因为

所以,当



知识点
已知数列



数列。
(1)若



(2)若存在正整数



正确答案
见解析。
解析
(1)依题意,
故
所以
令
则
①


所以
(2)因为
所以

故
又
所以
(ⅰ)当


(ⅱ)当


综上所述,当





知识点
扫码查看完整答案与解析