- 幂函数的概念、解析式、定义域、值域
- 共682题
在△



(1)求角
(2)求
正确答案
见解析
解析
解:(1)

所以

(2)
因为


故,

知识点
已知

(1)若

(2)若不等式


正确答案
见解析
解析
解:(1)若


当


当


又因为

当



当



故


(2)不等式

设



①当


当


当


从而
故,
②当

令



再令



取


所以,当


这与“
综上所述,
知识点
在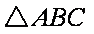
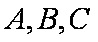
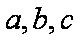

(1)求角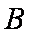
(2)如果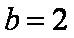
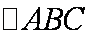
正确答案
见解析
解析
(1)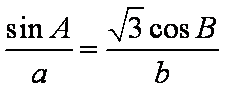
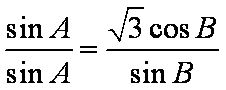
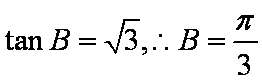
(2)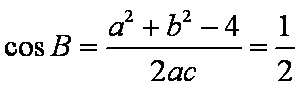
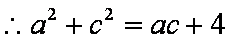
又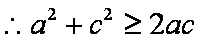
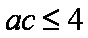
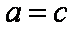
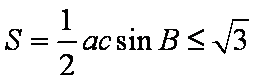
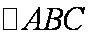
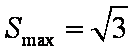
知识点
已知函数
(1)若


(2)若

正确答案
见解析。
解析
(1)函数


由

当









(2)设


由



















即
令
当









解法二:
设
设

当





当

设





当
由



知识点
已知函数
(1)求函数f(x) 的极值点;
(2)若直线 l过点(0,—1),并且与曲线 
(3)设函数


正确答案
见解析。
解析
(1)
而






所以


所以

(2)设切点坐标为

所以切线

又切线

解得
所以直线
(3)






所以


①当



所以

②当1<





③当



所以

综上,当



当

知识点
扫码查看完整答案与解析