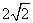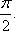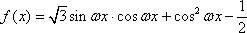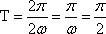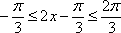- 幂函数的概念、解析式、定义域、值域
- 共682题
函数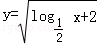
正确答案
(0,4]
解析
要使函数有意义,必有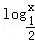
所以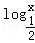
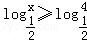
故答案为:(0,4]
知识点
已知函数

(1)求常数
(2)在











正确答案
见解析。
解析
(1)
∵ 
∵ 函数


∴当



此时,
(2)∵
∴
∴ 

∵ 
∴ 
∵ 
∴
即
由①和②解得
∵
∴
知识点
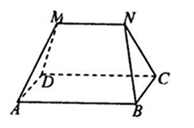
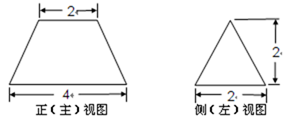
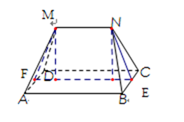
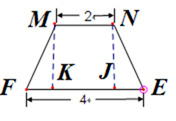
多面体MN-ABCD的底面ABCD为矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则AM的长
正确答案
解析
由正视图可知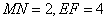
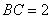
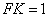
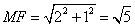
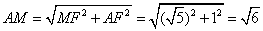
知识点
已知


(1)求函数

(2)是否存在整数






正确答案
见解析。
解析
(1)解:∵
∴
方程

当


故函数
当



则





故函数


单调递增区间为
(2)解:存在





一实数解,理由如下:
当



∴关于


当

得
若

若

若


当

当

∴


∵

∴方程

当



综上所述,对于任意




∴
知识点
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示。
(1)下表是年龄的频数分布表,求正整数
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率。
正确答案
见解析
解析
(1)由题设可知,

(2) 因为第1,2,3组共有50+50+200=300人,
利用分层抽样在300名学生中抽取
第1组的人数为
第2组的人数为
第3组的人数为
所以第1,2,3组分别抽取1人,1人,4人。………………6分
(2)设第1组的1位同学为





其中2人年龄都不在第3组的有:
所以至少有1人年龄在第3组的概率为
知识点
函数
正确答案
解析
略
知识点
已知函数
(1)讨论函数
(2)若对任意



正确答案
见解析。
解析
(1)
①当



②当




当



综上,当







(2)由题意知对任意

恒有
因为
由(1)知:当


所以
所以
因为

所以实数

知识点
正确答案
解析
略
知识点
已知函数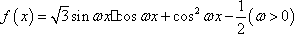
(1)求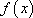
(2)将函数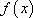
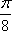
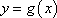

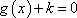
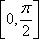
正确答案
见解析
解析
(1)
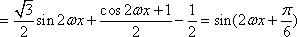
由题意知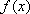
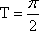
所以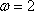
所以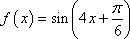
(2)将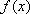
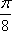
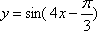
象所有点的横坐标伸长到原来的2倍,纵坐标不变,得到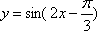
所以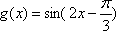
因为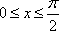
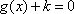
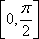
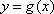
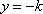
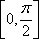
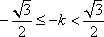
所以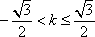
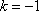
知识点
已知椭圆











(1)椭圆
(2)

正确答案
见解析
解析
(1)由题意可知





(2)设直线







即
∵

将①式代入②得:
当且仅当


知识点
扫码查看完整答案与解析