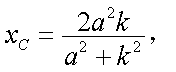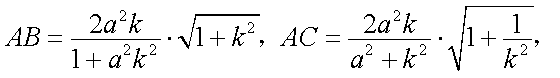- 幂函数的图像
- 共175题
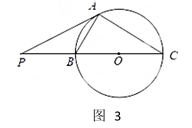
如图(3),
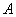
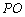
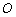
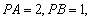

正确答案
解析
由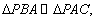
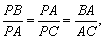

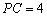
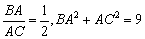
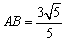
知识点
(1)证明:点P在C上;
(2)设点P关于点O的对称点为Q,证明:A、P、B、Q四点在同一圆上。
正确答案
见解析。
解析
知识点
已知


正确答案
解析


故
知识点
在平面直角坐标系



正确答案
2
解析
知识点
某班50名学生在一次百米测试中,成绩全部介于13秒与18
秒之间,将测试结果分成五组:每一组

…,第五组
图若成绩大于或等于14秒且小于16秒认为良好,则该班在这次
百米测试中成绩良好的人数等于__________人.
正确答案
27
解析
略
知识点
已知函数
(1)求
(2)设



(3)设





正确答案
见解析。
解析
(1)

列表如下:
∵g(1) = 1,∴y =
(2)当


∵



设


∴

设


即
设

∴
∴
设



∴


∴

∴a≥3 -


(3)由(1)知


∵

当


当



所以

此时


∴


由①②,得
∵

下证存在

取


设


∴


再证
∵

综上所述,

知识点
若将函数f(x)=sin2x+cos2x的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是( )
正确答案
解析
函数f(x)=sin2x+cos2x=

所得图象是函数y=

图象关于y轴对称,可得

即φ=﹣
当k=﹣1时,φ的最小正值是
知识点
函数y=log2x的图象大致是
正确答案
解析
本题考查对数函数的图象和基本性质.
知识点
已知抛物线C:



正确答案
解析
联立


不妨设A在y轴左侧,于是A,B的坐标分别为(-2,1),(4,4),
解法1:由抛物线的定义可得:


解法2:由抛物线的定义可得:
可求
∴
知识点
在平面直角坐标系xOy中,直角三角形ABC的三个顶点都在椭圆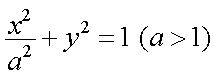
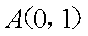
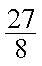
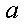
正确答案
3
解析
设AB的方程为: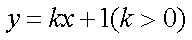
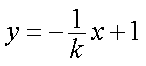
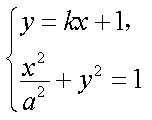
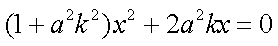
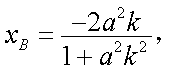
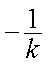
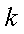
故
所以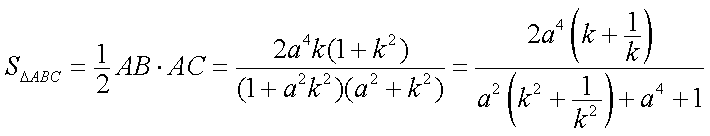
令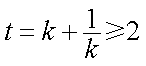
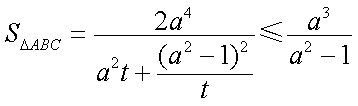
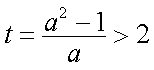
由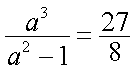
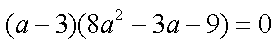
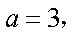
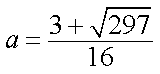
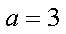
知识点
扫码查看完整答案与解析