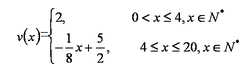- 幂函数的概念、解析式、定义域、值域
- 共682题
已知函数
(1)求
(2)设



(3)设





正确答案
见解析。
解析
(1)

列表如下:
∵g(1) = 1,∴y =
(2)当


∵



设


∴

设


即
设

∴
∴
设


∴


∴

∴a≥3 


(3)由(1)知


∵

当


当



所以

此时


∴


由①②,得
∵

下证存在

取


设


∴


再证
∵

综上所述,

知识点
第十八届省运会将于2014年9月在徐州市举办,为营造优美的环境,举办方决定在某“葫芦”形花坛中建喷泉,如图,该花坛的边界是两个半径为10米的圆弧围成,两圆心


(1)如图甲,在花坛中建矩形喷泉,四个顶点








(2)如图乙,在花坛中间铺设一条宽为2米的观赏长廊以作休闲之用,则矩形喷泉变为两个全等的等腰三角形,其中


正确答案
见解析。
解析
(1)在直角



所以矩形

令

则
令



列表如下:
所以当


(2)由(1)易得,喷泉的面积
由


所以
答:(1)矩形的宽

(2)喷泉的面积的取值范围是
知识点
如图,矩形ABCD的三个顶点A、B、C分别在函数


正确答案
解析
由







知识点
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点,研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度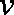
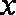
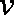
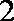
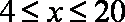
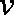
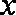
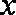
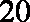
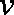

(1)当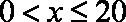
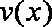
(2)当养殖密度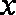
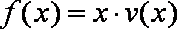
正确答案
(1)
(2)当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为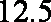
解析
解析:(1)由题意:当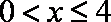
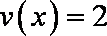
当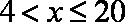
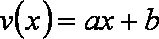
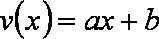
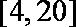
由已知得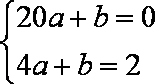
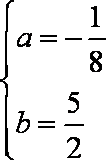
故函数
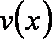
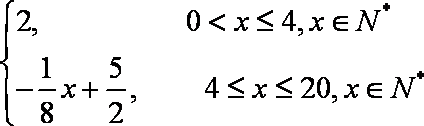
(2)依题意并由(1)可得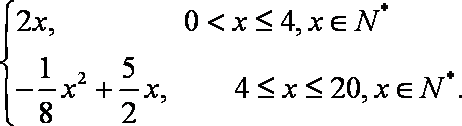
当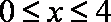
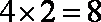
当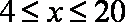
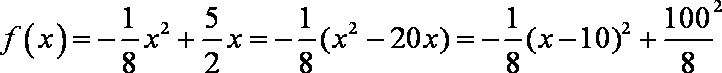
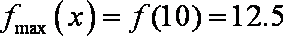
所以,当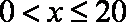
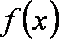
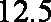
当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为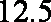
……………………………14分
知识点
在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形

















(1)试分别求出函数

(2)要使得点

正确答案
见解析
解析
解:(1)对于曲线


所以点



则
对于曲线


所以点



(2)因为




为
又



因为

故选用曲线




知识点
扫码查看完整答案与解析