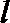- 两点间的距离公式
- 共14题
4.设点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.点

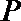
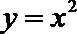
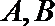
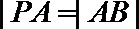
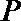
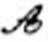
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知A、B两点分别在两条互相垂直的直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.曲线C:x|x|+y|y|=1
(I) 直线x+y-b=0与曲线C交于A,B两点用b表示|AB|的长;
(II) 分别过A,B作直线x+y=0的垂线,垂足分别为C,D,求四边形ABCD面积的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
直线y=kx+m(m≠0)与椭圆W:
(1)当点B的坐标为(0,1),且四边形OABC为菱形时,求AC的长;
(2)当点B在W上且不是W的顶点时,证明:四边形OABC不可能为菱形。
正确答案
见解析
解析
(1)因为四边形OABC为菱形,所以AC与OB相互垂直平分。
所以可设A


所以|AC|=
(2)假设四边形OABC为菱形。
因为点B不是W的顶点,且AC⊥OB,所以k≠0.
由
设A(x1,y1),C(x2,y2),
则

所以AC的中点为M
因为M为AC和OB的交点,且m≠0,k≠0,所以直线OB的斜率为
因为k·
所以四边形OABC不是菱形,与假设矛盾。
所以当点B不是W的顶点时,四边形OABC不可能是菱形。
知识点
已知两定点





①


正确答案
①④
解析
略
知识点
在直角坐标系







(1)求曲线

(2) 设




正确答案
见解析
解析
(1)由曲线

两式两边平方相加得:
即曲线
由曲线

即
即曲线

(2)由(1)知椭圆



所以当




知识点
在直角坐标系







(1)求曲线

(2)求曲线

正确答案
(1)C1:x2+(y-1)2=1,C2:x-y+1=0
(2)1
解析
(1)将


将

(2) 由(1)知曲线






知识点
14.已知点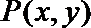
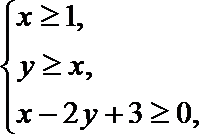
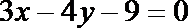
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析