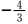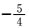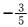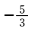直线的倾斜角与斜率_章节学习

1

题型：单选题

|

单选题 · 5 分

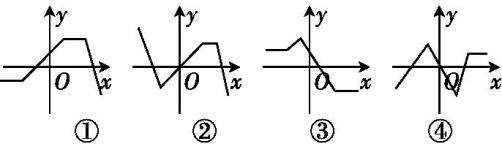
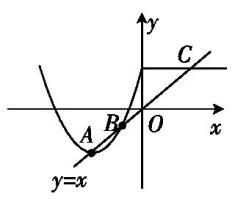
6.下列四个函数图象，只有一个是符合y=|k1x+b1|+|k2x+b2|-|k3x+b3|（其中k1，k2，k3为正实数，b1，b2，b3为非零实数）的图象，则根据你所判断的图象，k1，k2，k3之间一定成立的关系是（）

Ak1+k2=k3

Bk1=k2=k3

Ck1+k2>k3

Dk1+k2<k3

正确答案

A

解析

当x足够小时，y=-(k1+k2-k3)x-(b1+b2-b3)

当x足够大时，y=(k1+k2-k3)x+(b1+b2-b3)

可见折线的两端的斜率必定为相反数，此时只有③符合条件.

此时k1+k2-k3=0.

知识点

函数的图象直线的倾斜角与斜率

1

题型：填空题

|

填空题 · 5 分

9.过点(，0)引直线l与曲线y=相交于A、B两点，O为坐标原点，当△AOB的面积取最大值时，直线l的斜率为　　　　。

正确答案

解析

如图，

∵S△AOB=|OA|·|OB|·sin∠AOB=sin∠AOB≤，

当∠AOB=时，S△AOB面积最大，

此时点O到AB的距离d=.

设AB的方程为y=k(x－)(k<0)，即kx－y－k=0，

由d==，得k=－.

知识点

直线的倾斜角与斜率直线与圆相交的性质

1

题型：单选题

|

单选题 · 5 分

2.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx+2上至少存在一点使得以该点为圆心,1为半径的圆与圆C 有公共点,则k的最小值是（）

A

B

C

D

正确答案

A

解析

∵圆C的方程为x2+y2-8x+15=0,整理得(x-4)2+y2=1,即圆C是以(4,0)为圆心,1为半径的圆.又直线y=kx+2上至少存在一点使得以该点为圆心,1为半径的圆与圆C有公共点,∴只需圆C的圆心(4,0)到直线y=kx+2的距离d不大于2即可.

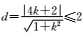
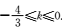
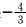
又,即3k2+4k≤0,∴.∴k的最小值是。

知识点

直线的倾斜角与斜率

1

题型：单选题

|

单选题 · 5 分

6.设方程x4+ax-4=0的各实根为x1,x2,…,xk(k≤4)。若点(xi, )(i=1,2,…,k)均在直线y=x的异侧，则实数a的取值范围是（）

A(-6,6)

B[-6,6]

C(-4,4)

D[-4,4]

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

函数零点的判断和求解直线的倾斜角与斜率

1

题型：单选题

|

单选题 · 5 分

3.已知直线l的倾斜角为α，且0°≤α≤135°，则直线l的斜率取值范围为（）

A(－∞，1)

B(－∞，－1]∪[0，+∞)

C[0，+∞)

D(－1，+∞)

正确答案

B

解析

　　当α从0°无限接近90°时，斜率取值范围为[0，+∞)；当从90°无限接近135°时，斜率取值范围为(-∞，－1].

知识点

直线的倾斜角与斜率

1

题型：单选题

|

单选题 · 5 分

5.过点M(-2，0)的直线l与椭圆x2+2y2=2交于P1，P2，线段P1P2的中点为P。设直线l的斜率为k1(k1≠0)，直线OP(O为坐标原点)的斜率为k2，则k1k2等于（）

A- 2

B2

C-

D

正确答案

C

解析

设P1(x1，y1)，P2(x2，y2)，P(x0，y0)，则=2，=2

两式作差得=0

∴k1==－=-

又k2=，∴k1k2=- ，故选C.

知识点

直线的倾斜角与斜率椭圆的几何性质直线与圆锥曲线的综合问题

1

题型：填空题

|

填空题 · 5 分

7.经过点P(0，-1)作直线l，若直线l与连接A(1，-2)，B(2，1)的线段总有公共点，则直线l的斜率k和倾斜角α的取值范围分别为　　　　和　　　　。

正确答案

[-1，1]；[0，]∪[，π)

解析

如图所示，结合图形，

为使直线l与线段AB总有公共点，则kPA≤k≤kPB，而kPB>0，kPA<0

故当k<0时，倾斜角α为钝角

当k=0时，α=0，当k>0时，α为锐角.

又kPA==-1，

kPB==1，

∴-1≤k≤1，即直线l的斜率k的取值范围为[-1，1].

又当0≤k≤1时，0≤α≤，

当-1≤k<0时，≤α<π，

∴直线l的倾斜角α的取值范围为[0，]∪[，π).

知识点

直线的倾斜角与斜率

1

题型：单选题

|

单选题 · 5 分

4．函数f（x）＝x cosx在点（0，f（0））处的切线斜率是

A0

B－1

C1

D

正确答案

C

解析

f’(x)=cosx-xsinx,得k=f’（0）=1。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查导数的几何意义

解题思路

直接求导，即可得到结果。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

易错点

本题易在求导数时发生错误。

知识点

导数的几何意义直线的倾斜角与斜率

1

题型：简答题

|

简答题 · 12 分

20．已知椭圆C：=1（a>0，b>0）的两焦点与短轴的一个端点的连线构成等边三角形，直线x+y+2一1=0与以椭圆C的右焦点为圆心，以椭圆的长半轴长为半径的圆相切．

(I)求椭圆C的方程；

(Ⅱ)设点B，C，D是椭圆上不同于椭圆顶点的三点，点B与点D关于原点O对称．设直线CD，CB，OB，OC的斜率分别为k1，k2，k3，k4，且k1k2=k3k4．

(i)求k1k2的值：

(ii)求OB2+ OC2的值．

正确答案

（I）所求椭圆方程为；

(Ⅱ) (i)k1k2；

(ii)OB2+ OC2=7

解析

试题分析：本题属于直线与圆锥曲线的综合问题，属于较难类型，主要在于计算，具体解析如下：

（Ⅰ）设椭圆的右焦点，则

由题意，以椭圆的右焦点为圆心，以椭圆的长半轴长为半径的圆的方程为，

∴圆心到直线的距离

（*）

∵椭圆的两焦点与短轴的一个端点的连线构成等边三角形，

∴,，代入（*）式得，，

故所求椭圆方程为

（Ⅱ）（i）设，则，

于是

（ii）方法一由（i）知，，故．

所以，

即，所以，．

又，故．

所以，OB2+OC2 ．

方法二由（i）知，．将直线方程代入椭圆中，

得．同理，．

所以，．

下同方法一

考查方向

本题考查了圆锥曲线中的有关问题，大体可以分成以下几类：

1、椭圆标准方程的求法；

2、点到直线距离公式的应用；

3、直线、圆及圆锥曲线的交汇问题；

4、运算能力的考察。

解题思路

本题考查圆锥曲线的综合问题，难度稍微有些大，问题最大的在于计算，解题步骤如下：

1、根据条件，利用点到直线的距离公式得出基本量a,b,c的关系，进而写出椭圆方程；

2、直接利用斜率的表达式计算出k1k2；

3、此时方法不唯一，可以利用方程间的未知数的关系直接求出各个量的值，进而求出OB2+ OC2=7；也可以把直线方程代入椭圆方程表示出，，进而求出OB2+ OC2=7。

易错点

1、题目分析得到基本量a,b,c的关系时出错；

2、k1k2的表达式写错；

3、直线方程代入椭圆方程后，计算OB2+ OC2出错。

知识点

直线的倾斜角与斜率椭圆的定义及标准方程圆锥曲线的定点、定值问题

1

题型：单选题

|

单选题 · 5 分

11．已知点P在直线x+3y-2=0上，点Q在直线x+3y+6=0上，线段PQ的中点为M(x0，y0)，且y00 +2，则的取值范围是（）

A[一，0）

B（一，0）

C（一，+∞）

D（一∞，一）（0,+∞)

正确答案

D

解析

因为PQ的中点为M，可以得出点M的轨迹就是x+3y+2=0与直线x+3y+6=0间的平行直线x+3y+2=0；又因为y00 +2，可知点(x0，y0)满足在直线x-y+2=0的右下部分。

由求出点M（-2,0）

则，而直线x+3y+6=0的斜率为

所以的取值范围是（一∞，一）（0,+∞)

A选项不正确，B选项不正确，C选项不正确，所以选D选项。

考查方向

本题主要考查了两条平行线间的距离，两条直线的交点坐标，直线斜率的求法等知识,在近几年的各省高考题出现的频率较高，经常和线性规划，不等式等知识结合出题。

解题思路

1、首先由直线x+3y+2=0与直线x+3y+6=0是平行线，得出PQ的中点M(x0，y0)满足的直线方程；

2、根据y0<x0 +2求出对应的射线范围，即进一步限定点M的范围；

3、结合的几何意义求出它的范围。

A选项不正确， B选项不正确， C选项不正确，D选项正确。

易错点

1、本题不容易想到点M的轨迹就是与直线x+3y-2=0和x+3y+6=0等距离的直线。

2、本题在求解出直线与x+3y+2=0与直线x-y+2=0的交点后，求解斜率的范围时候容易出错。

3、端点处的讨论容易考虑不全。

知识点

直线的倾斜角与斜率

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点